.
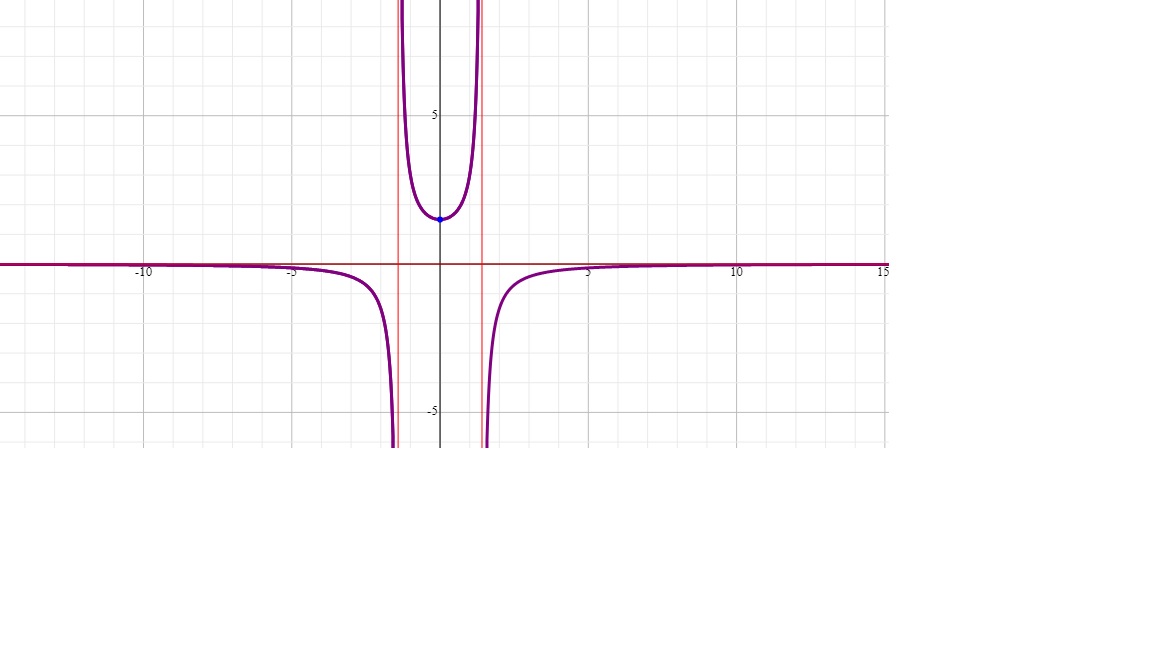
y=3/(2-x^2)
We know that, in a rational function, at the x-values where the denominator becomes 0 the function becomes undefined. At those locations, we have vertical asymptotes.
2-x^2=0, :. x=+-sqrt2
Therefore, the function's domain will be in three pieces:
(-oo < x < -sqrt2) and (-sqrt2 < x < sqrt2) and (sqrt2 < x < oo)
Because the degree of the denominator is higher than the degree of the numerator, the x-axis is the horizontal asymptote. And because the numerator is a constant, y can never be 0. This means the range of the function is not one piece. Rather, it is in two or more pieces. We need to examine the function more closely.
For all x-values in the part of the domain (-oo < x < -sqrt2), the function is always negative and its range is:
0 > y > -oo
For the x-values in the part of the domain (sqrt2 < x < oo), the function is always negative and its range is:
-oo < y < 0
For x-values in the part of the domain (-sqrt2 < x < sqrt2), the function is always positive. It means this piece of the function has to have both ends of it going to oo, i.e. at -sqrt2 and sqrt2.
Then, it must be U-shaped and therefore must have a minimum point. We know y can not be 0. As such, the minimum point must be somewhere above y=0.
The function becomes minimum when its denominator reaches its maximum value. The maximum value of 2-x^2 is when x^2=0 which means x=0 and y=3/2. Therefore, the range of the function is:
0 > y > -oo and 3/2 <= y < oo
The following is the graph of the function where the domain and range identified above become obvious: