Find the root of the equation. Give your answers correct to six decimal places?
#x^3-x=2#
(a) Use Newton's method with x1 = 1.
(b) Solve the equation using x1 = 0.6 as the initial approximation.
(c) Solve the equation using x1 = 0.58. (You definitely need a programmable calculator for this part.)
(a) Use Newton's method with x1 = 1.
(b) Solve the equation using x1 = 0.6 as the initial approximation.
(c) Solve the equation using x1 = 0.58. (You definitely need a programmable calculator for this part.)
1 Answer
The solution is
Explanation:
We have:
Let
# x_(n+1) = x_n - f(x_n) / (f'(x_n)) #
# :. x_(n+1) = x_n - (x_n^3-x_n-2) / (3x_n^2-1) #
(a) If we start with
So we see that very rapidly the Newton-Rhapson method converges to the solution
.

(b) If we start with
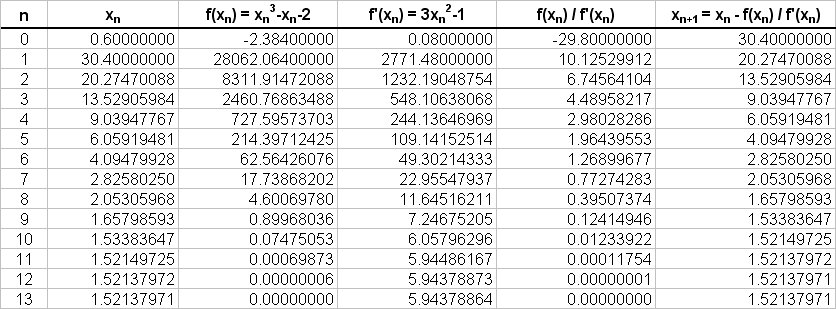
So again we see that the Newton-Rhapson method converges to the solution
(c) If we start with
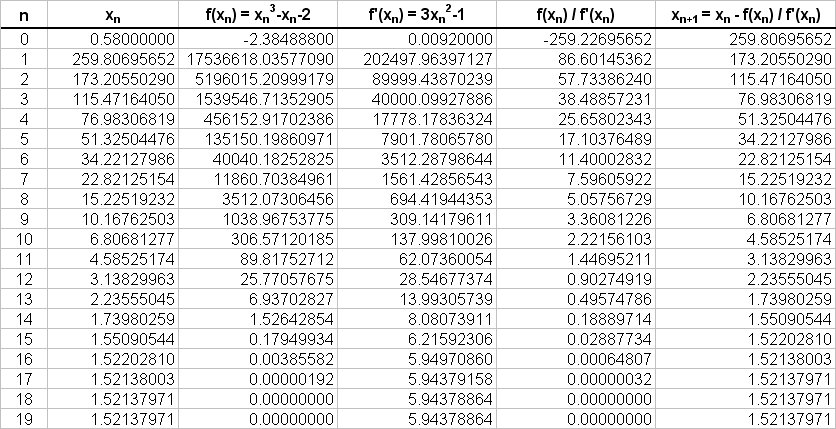
So again we see that the Newton-Rhapson method converges to the solution

