Find the set of values of k,where k is a constant,when equation x^3-12x^2+45x-34=k has (a) one root (b) three roots?
1 Answer
Explanation:
.
We know that this is a cubic function and ordinarily would have three roots, i.e. it would cross the
We also know that a cubic function typically has one maximum and one minimum unless the function is a perfect cubic in which case it would cross the
A perfect cubic function would be in the form of:
If we expand this we would get:
Setting the corresponding coefficients equal to each other, we get:
This set of three equation does not have a solution as is evident. Therefore, our function can not be a perfect cubic. This means it has a minimum and a maximum and an inflection point.
In order for it to have one root, it would have to cross the
Let's find these points. We will take the derivative of the function and set it equal to
Let's plug them into the function to find their
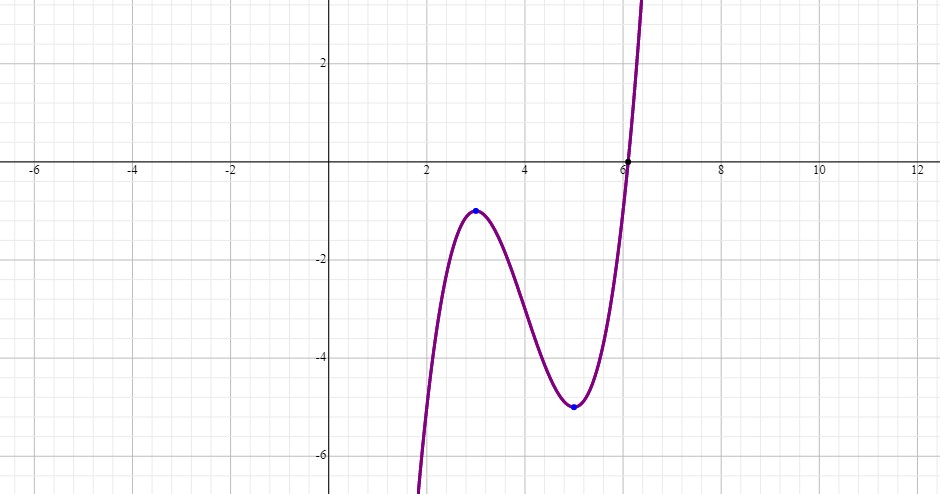
For these points to be above the
We have to go with
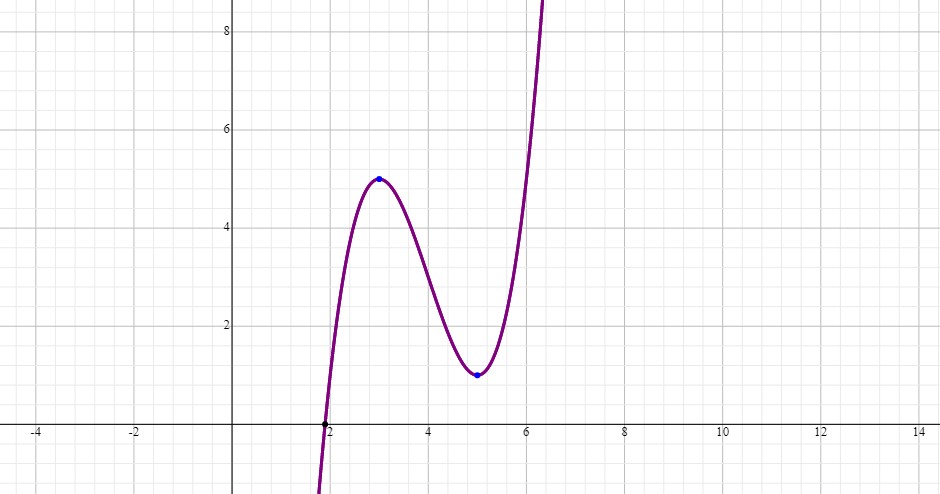
For the points to be below the
We have to go with
Therefore, the condition for one root is:
For the function to have three roots,
Please note that if
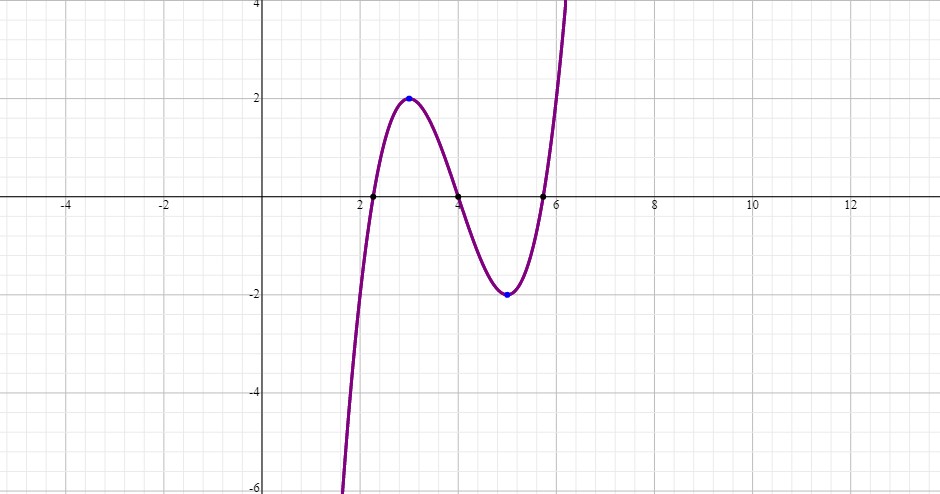
The following graph is drawn for
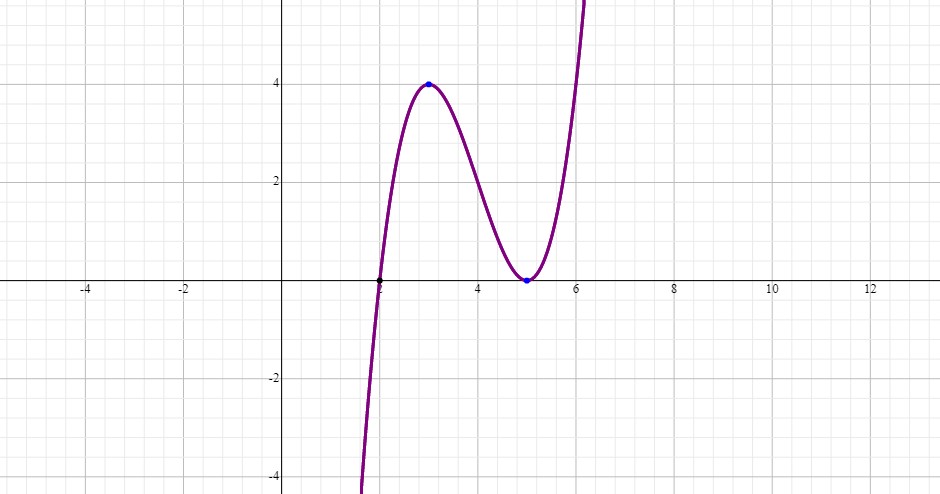
The following graph is drawn for
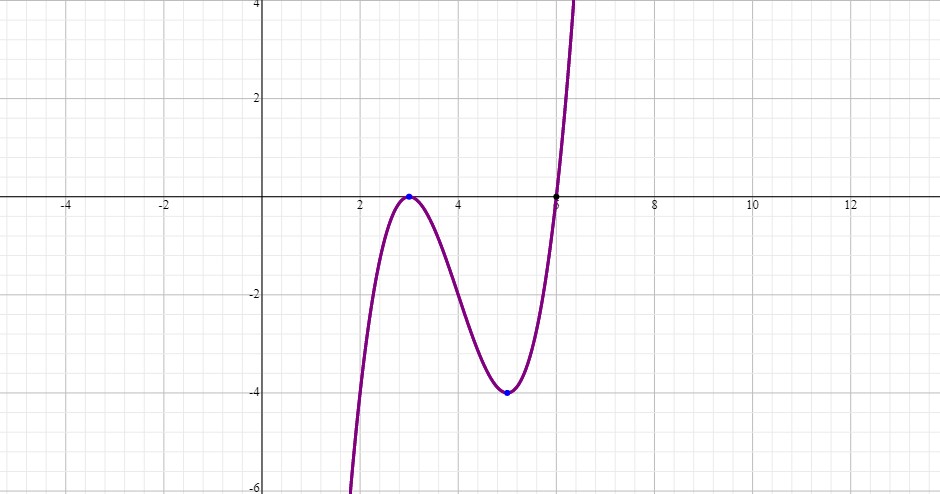
Therefore,