Find the value of the line integral. F · dr (Hint: If F is conservative, the integration may be easier on an alternative path.) (2x − 8y + 6) dx − (8x + y − 6) dy?
part c:
part c:

1 Answer
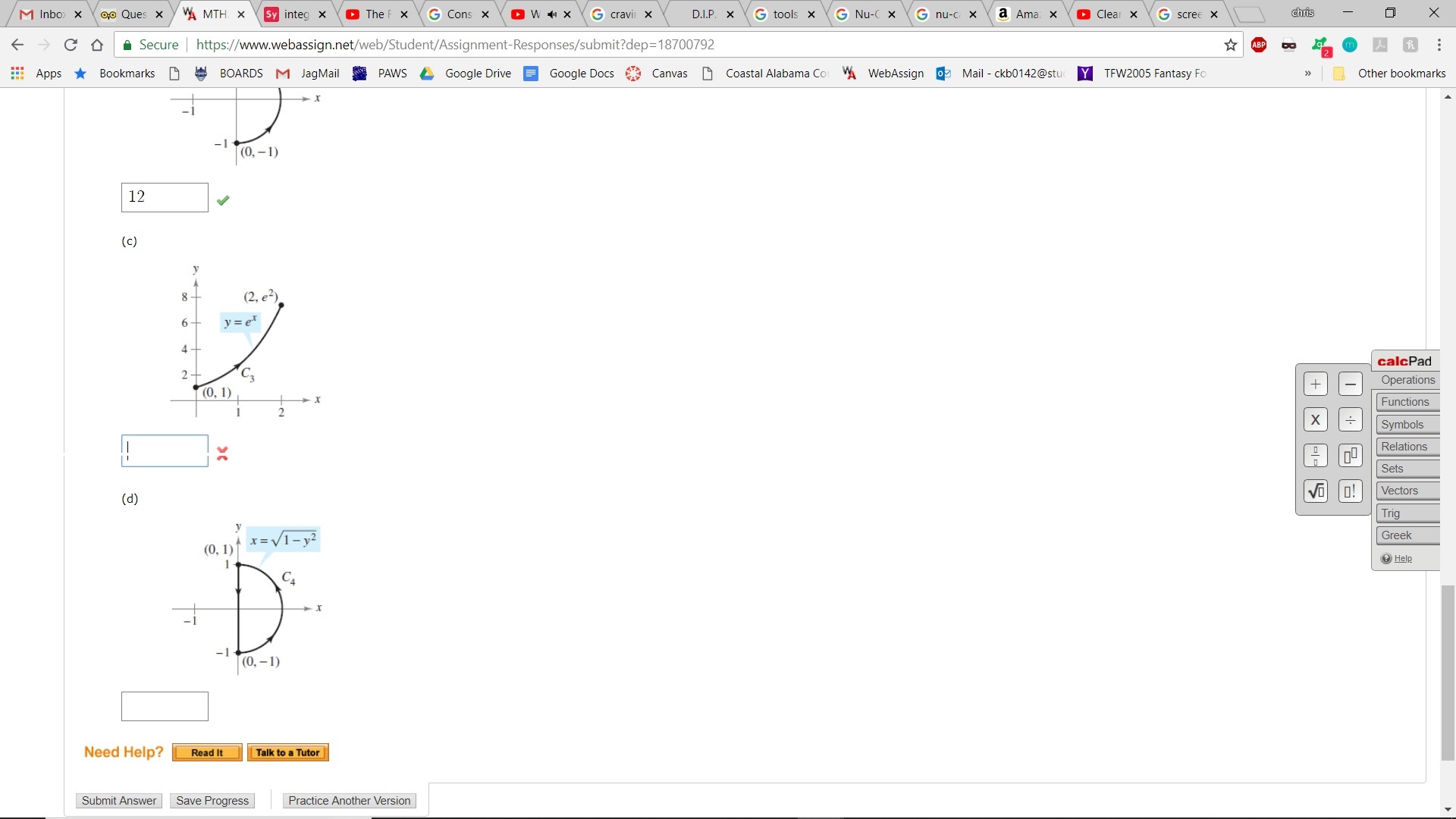
(c)
(d)
Explanation:
If you mean that the line integral is:
Then
And
So
You can only see (c) and (d) in the screengrab
- (c)
Along
That looks ugly so just use a different 2-step path:
-
#{(bbbA: qquad dx = 0, x = 0, y: \ 1 to e^2 ),(bbbB: qquad dy = 0, y = e^2, x: \ 0 to 2 ):}# -
Path
#bbbA#
- Path
#bbbB#
- (d)
Zero, because this is a closed path and the field is conservative

