.
y=0 is the x-axis. As such, we want to revolve the area between the curve of y=sinx, the x-axis , x=pi/2, and x=pi around the x-axis and calculate the volume of the solid generated.
The graph below shows this area:
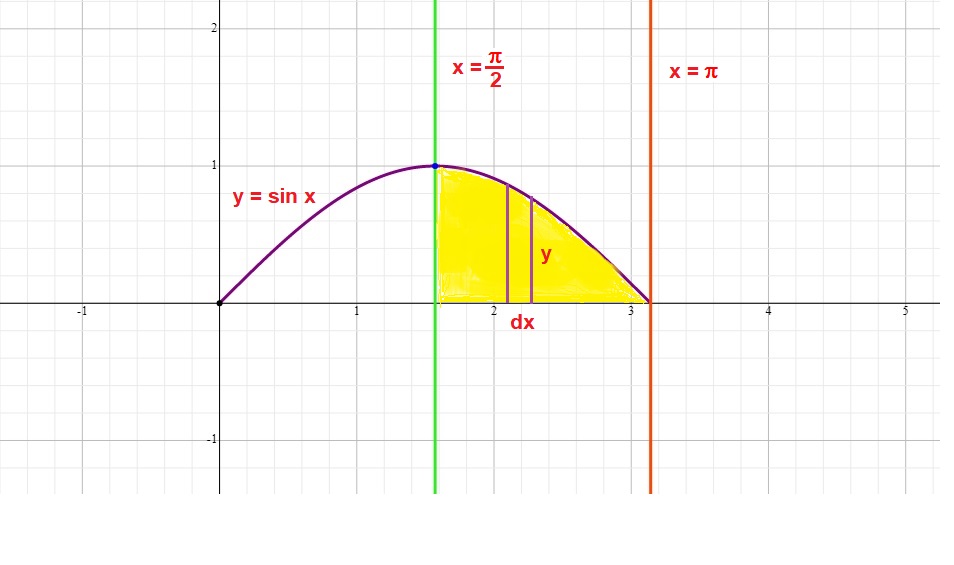
If we revolve this area around the x-axis we will get the solid shown below:
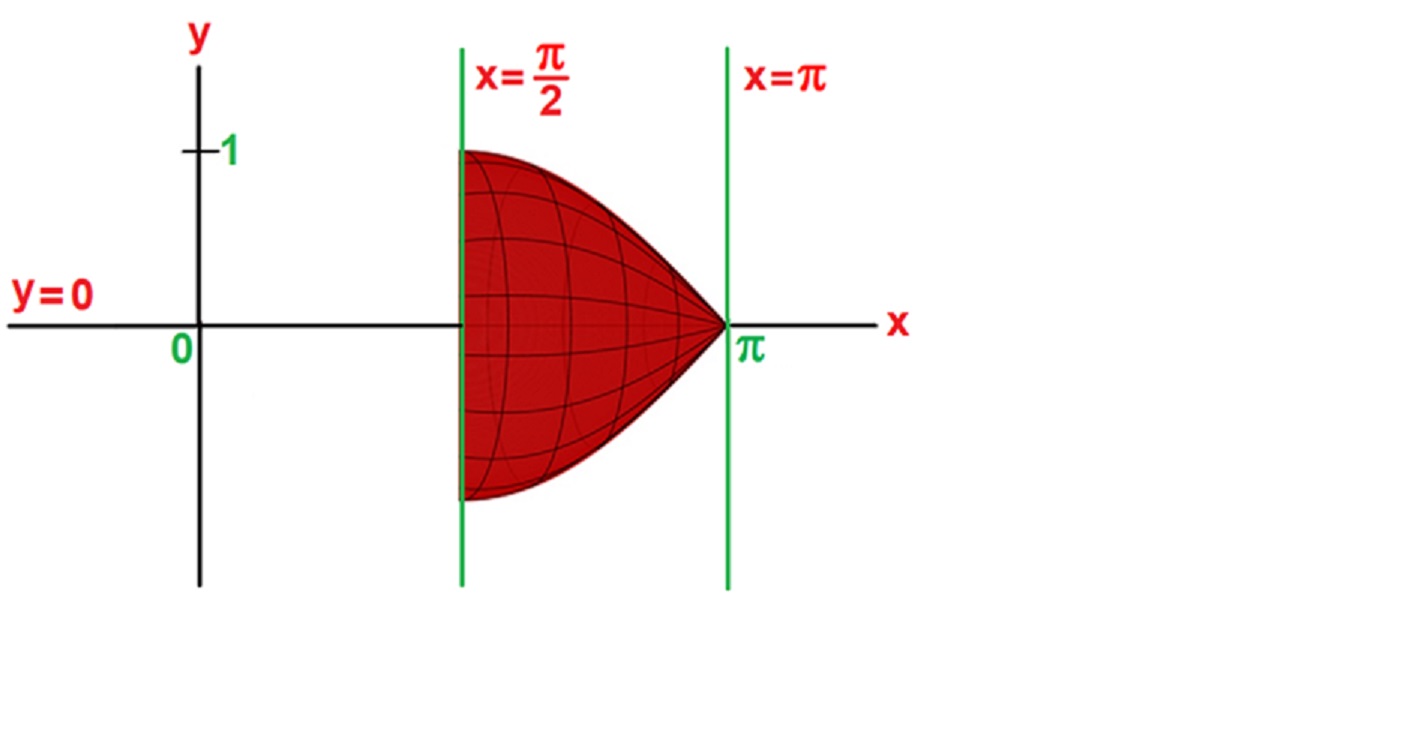
If you can imagine this solid being divided into vertical slices parallel to the y-axis with a extremely small thicknesses each one would look like a thin disc with the surface area of a circle and thickness of dx.
The circles have a radius r that is equal to y=sinx and vary in size depending on where on the x-axis you perform the slice.
So, because the formula for the area of a circle is A=pir^2,, we can calculate the area of each disc as:
A=pisin^2x
Now if we take the integral of this function and evaluate it between pi/2 and pi we will have the volume of the solid.
This is because the integral adds the areas of infinite number of discs between the two limits together.
V=int_(pi/2)^pipisin^2xdx=piint_(pi/2)^pi(1-cos2x)/2dx
V=pi/2int_(pi/2)^pidx-pi/2int_(pi/2)^picos2xdx
V=pi/2x-pi/2I
I=int_(pi/2)^picos2xdx
Let u=2x
du=2dx
dx=(du)/2
Let's substitute:
I=intcosu(du)/2=1/2intcosudu=1/2sinu=1/2sin2x
Let's plug this in:
V=pi/2x-pi/2*1/2sin2x=(pi/4(2x-sin2x))_(pi/2)^pi
V=pi/4(2pi-sin2pi-pi+sinpi)
V=pi/4(pi-0+0)
V=pi^2/4



