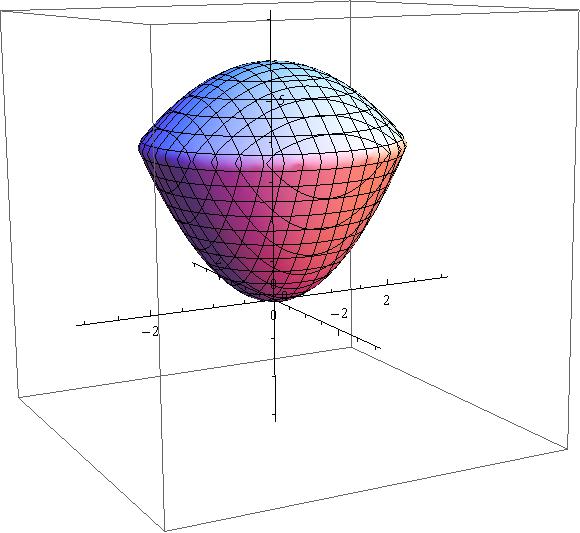
Find the volume of the region bounded by y=sqrt(z-x^2) and x^2+y^2+2z=12?
find the volume of the region bounded by y=sqrt(z-x^2) and x^2+y^2+2z=12?
find the volume of the region bounded by y=sqrt(z-x^2) and x^2+y^2+2z=12?
2 Answers
Explanation:
this is symmetric about z axis so we use polar co-ords
first paraboloid
second
(and
here is a 2-D plot:
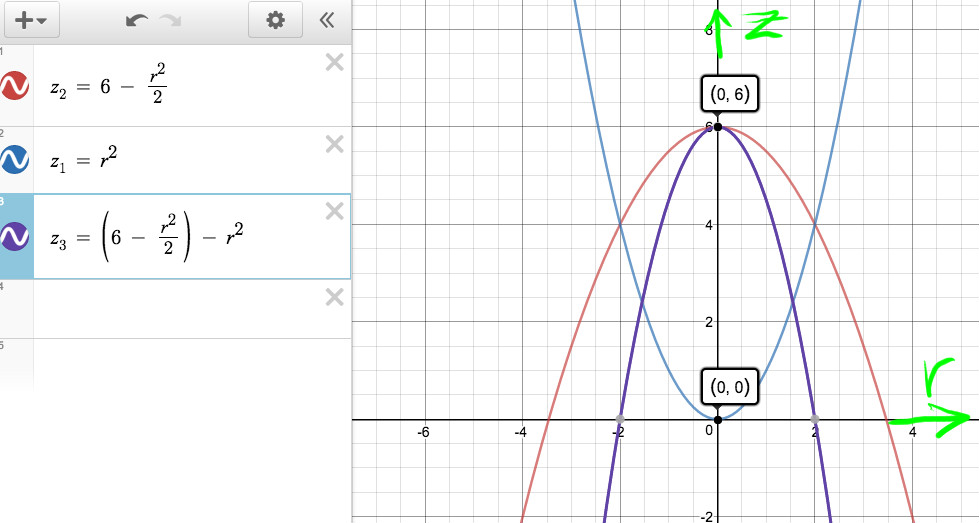
We need to find the volume that is made by revolving the area between the red and blue curves around the z-axis. That is the area under the purple curve, which is entered as
Ie, we need to find volume
where volume element in polar is
As an aside, @abubakar wanted this expressed as a triple integral . I originally skipped that step because it just adds extra notation but if we start with the general volume element and switching straight to cylindrical co-ordinates, we can say that
now neither r or z depend upon
I did that to simplify the next bit, because we have
In general terms, to do this we need either do
OR
The explanation and drawings here are helpful
The key to this is that these are iterated integrals. The
A graphic contribution.
Explanation:
A graphic contribution.