Find the volume of the solid by using cylindrical shells?

1 Answer
Explanation:
the volume by cylindrical shell method when the curve rotating about the
but the area enclosed by the curve lies in the first quadrant.
so
lets find the interval of integral.
the interval of the integral
now let set up the integral:
show below the region revolving (shaded region) :
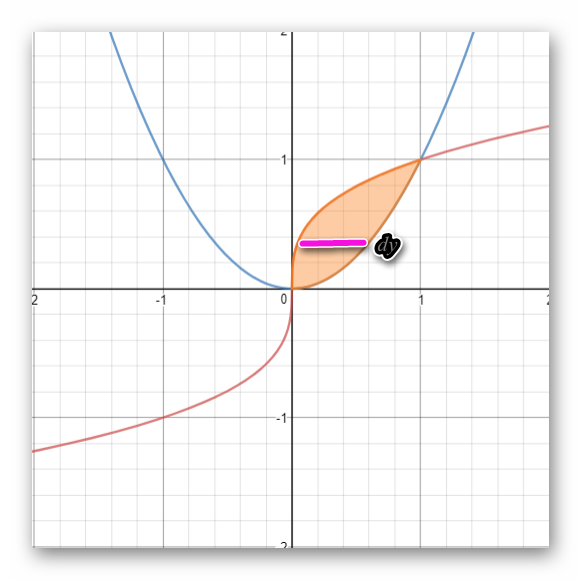
show the link below that will help you to understand how to find the volume by cylindrical shell method:
cylindrical shell method

