Find the volume of the solid obtained by revolving the curve x=acos^(3)θ,y=asin^(3)θ about the y-axis?

Question

7061 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-04-17T09:52:17

#V = (32 pi a^3)/105#

#x=acos^(3)θ,y=asin^(3)θ#

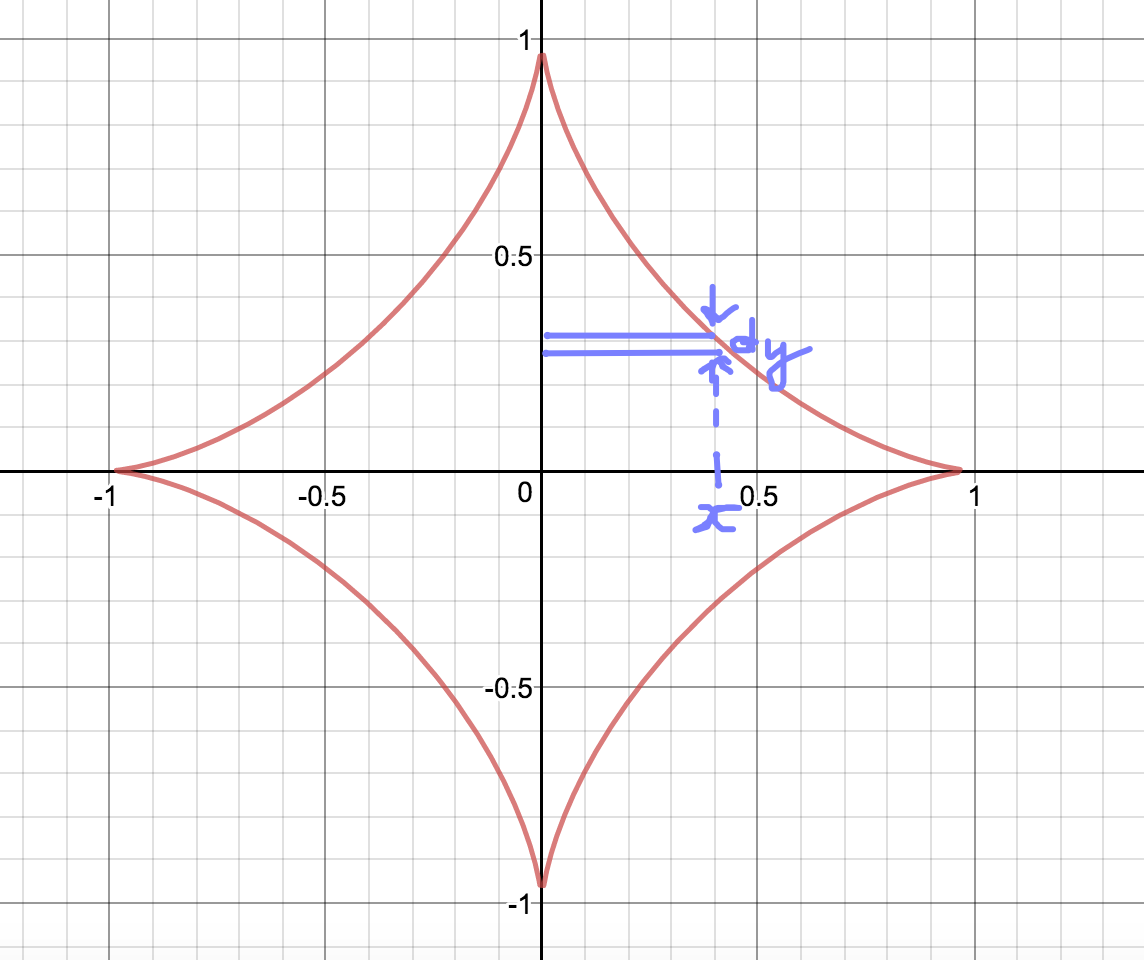
Desmos plot with a = 1

Consider the disc of height #dy#, revolved about the y - axis. It has radius #x# and so volume:

#dV = pi x^2 dy implies V = pi int_(y = -a)^a x^2 \ dy#

Using the parameterisation:

# V = pi int_( -pi/2)^(pi/2) (acos^(3)θ)^2 d(asin^(3)θ)#

#= 3 pi a^3 int_( -pi/2)^(pi/2) \ cos^(7)θ \ sin^(2)θ \ d theta#

#= (32 pi a^3)/105#, computer solution.

[It can be integrated by hand using trig ID's etc.]