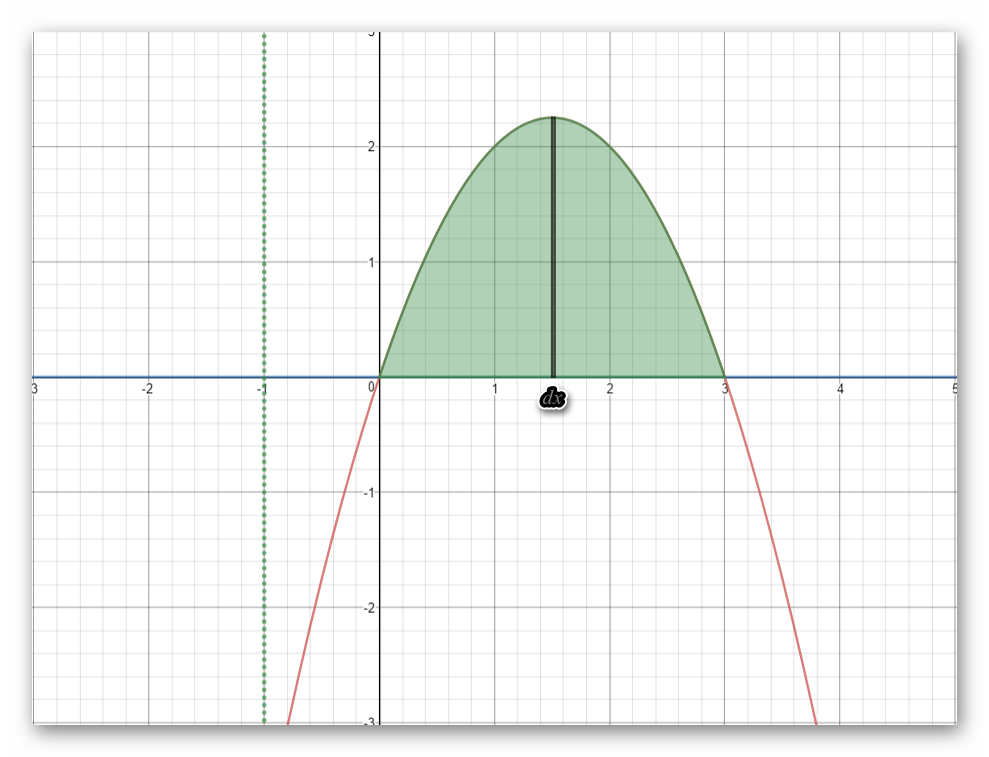
Find the volume using cylindrical shells? (Enclosed by x-axis and parabola #y=3x-x^2#, revolved about #x=-1#)
So far, I have the bounds at 0 and 3.
...I think I've forgotten how to apply shells, exactly.
Assuming thickness is #dx# , and height is the area given (#3x-x^2# )... then what is the radius? I don't know what that would be (is it #x# ?)
What I have, plugged into equation:
#V=2\pi\int_0^3[r*(3-x^2)dx]#
So far, I have the bounds at 0 and 3.
...I think I've forgotten how to apply shells, exactly.
Assuming thickness is
What I have, plugged into equation:
1 Answer
Explanation:
In cylindrical shell method the slice should be parallel to the axis of revolution.
In your question the area bounded revolving around
where
show below the region (shaded) revolving around