Find #y′′# for the curve #ln(x) + y = ln(x^2) − y^2# at #y = 0#?

Question

1792 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-01-04T20:15:34

#x = 1#, when #y = 0#

#y''(1) = -3#

Given:

#ln(x) + y = ln(x^2) − y^2#

Add #y^2-ln(x)# to both sides:

#y^2 + y = ln(x^2) − ln(x)#

Use the fact that subtraction of logarithms is the as division within the argument:

#y^2 + y = ln(x^2/x)#

#y^2 + y = ln(x)#

Write is standard quadratic form:

#y^2 + y - ln(x)=0" [1]"#

Here is a graph of equation [1]:

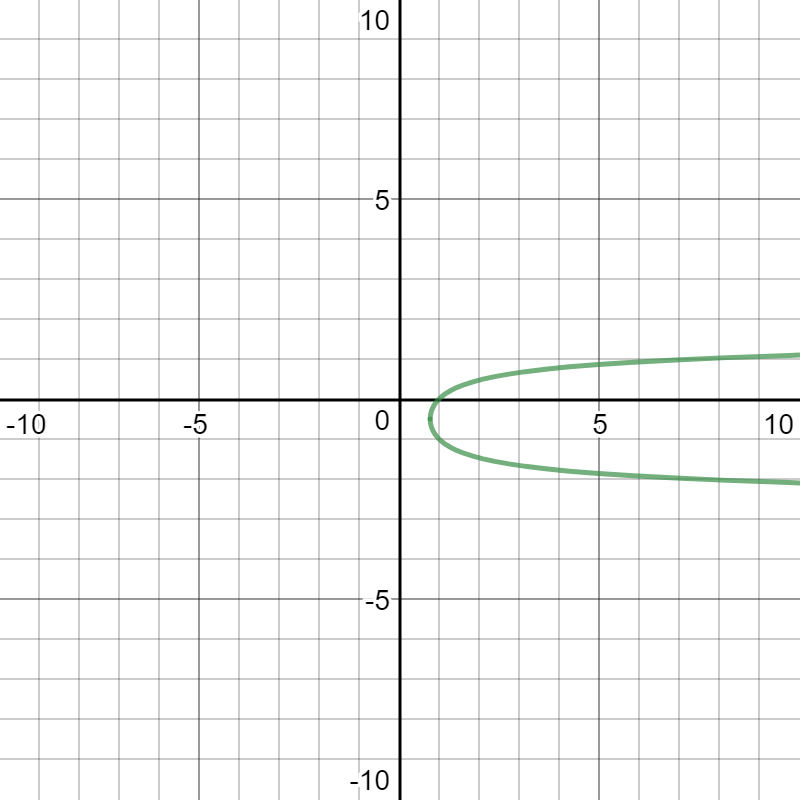
www.desmos.com/calculator

We can use the quadratic formula to obtain two equations of y in terms of x

#y = -1/2+ sqrt(1+4ln(x))/2" [1a]"#

and

#y = -1/2-sqrt(1+4ln(x))/2" [1b]"#

Here are the graphs of equations [1a] and [1b]:

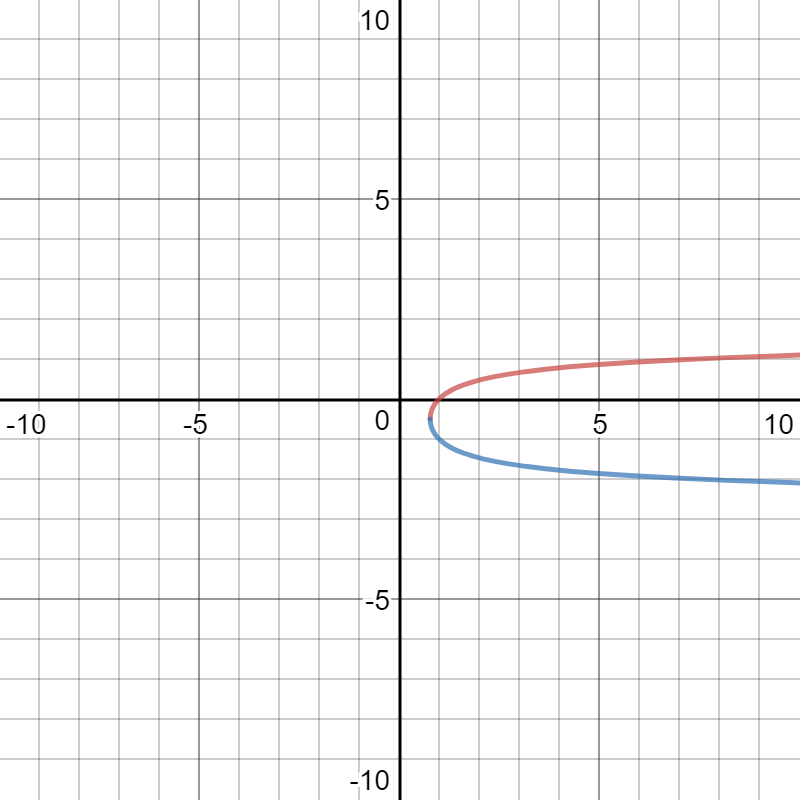
www.desmos.com/calculator

Please observe that equation [1a] contains the point of interest, #(1,0)#, therefore, we shall only be differentiating this equation.

#y' = 1/(xsqrt(4ln(x)+1))#

#y''= -(4ln(x)+3)/(x^2(4ln(x)+1)^(3/2)#

Evaluate when #y = 0# and #x=1#:

#y''(1) = -3#