Finding and sketching the locus of a complex number?

enter image source here

1 Answer
Steve M
Sep 10, 2017

We have:

# z = 2cos theta + i(1-2sin theta) #

Part (i)

# abs( z-i ) = abs( 2cos theta + i(1-2sin theta) - i ) #
# \ \ \ \ \ \ \ \ \ \= abs( 2cos theta + i-2isin theta - i ) #
# \ \ \ \ \ \ \ \ \ \= abs( 2cos theta -2isin theta ) #
# \ \ \ \ \ \ \ \ \ \= sqrt( (2cos theta)^2 + (-2sin theta)^2 ) #
# \ \ \ \ \ \ \ \ \ \= sqrt( (2cos theta)^2 + (2sin theta)^2 ) #
# \ \ \ \ \ \ \ \ \ \= sqrt( 2^2cos^2 theta + 2^2sin^2 theta ) #
# \ \ \ \ \ \ \ \ \ \= sqrt( 2^2(cos^2 theta + sin^2 theta) ) #
# \ \ \ \ \ \ \ \ \ \= sqrt( 2^2 ) #
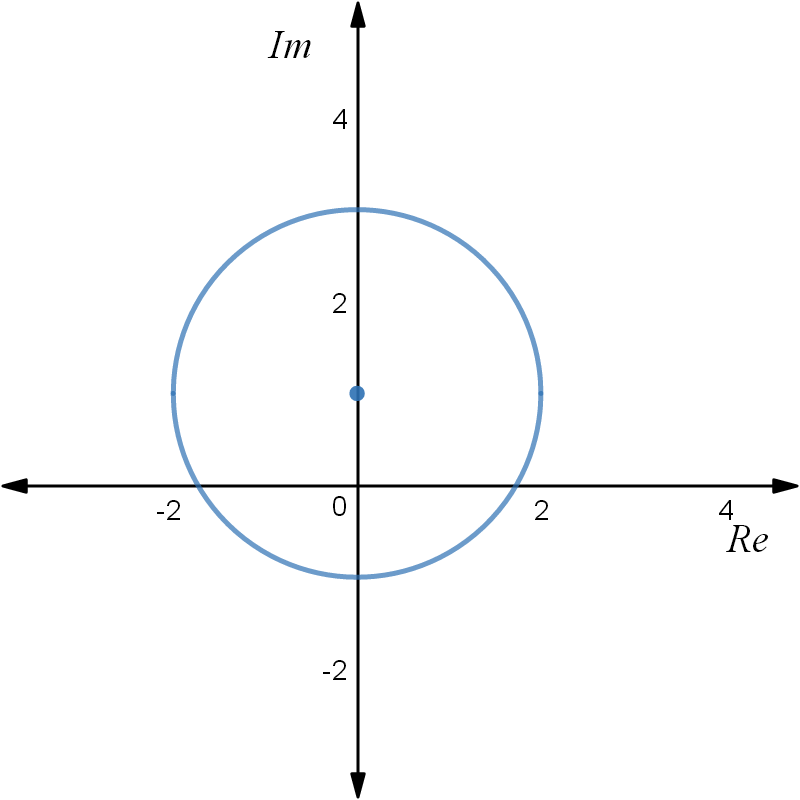
# \ \ \ \ \ \ \ \ \ \= 2 # QED

This locus represents a circle centred on #(0+i)# and radius #2#, The locus is shown in the following plot on the Argand diagram:

www.desmos.com

Part (ii)

# 1/(z+2-i) = 1/(2cos theta + i(1-2sin theta)+2-i)#
# \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = 1/(2cos theta + i-2isin theta+2-i)#
# \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = 1/(2+ 2cos theta -2isin theta)#
# \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = 1/(2+ 2cos theta -2isin theta).(2+ 2cos theta +2isin theta)/(2+ 2cos theta +2isin theta)#

# \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = (2+ 2cos theta +2isin theta)/( (2+ 2cos theta)^2 -(2isin theta)^2 )#

# \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = (2+ 2cos theta +2isin theta)/( 4+8costheta+4cos^2theta +4sin^2theta )#

# \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = (2+ 2cos theta +2isin theta)/( 4+8costheta+4 )#

# \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = (2+ 2cos theta +2isin theta)/( 8+8costheta)#

# \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = (2+ 2cos theta)/(8+8costheta) +(2isin theta)/( 8+8costheta)#

And so:

# Re{1/(z+2-i)} = (2+ 2cos theta)/(8+8costheta) #
# \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = (2(1+ cos theta))/(8(1+costheta)) #

# \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = 1/4 #, a constant, QED

Related questions
Impact of this question
2867 views around the world
You can reuse this answer
Creative Commons License