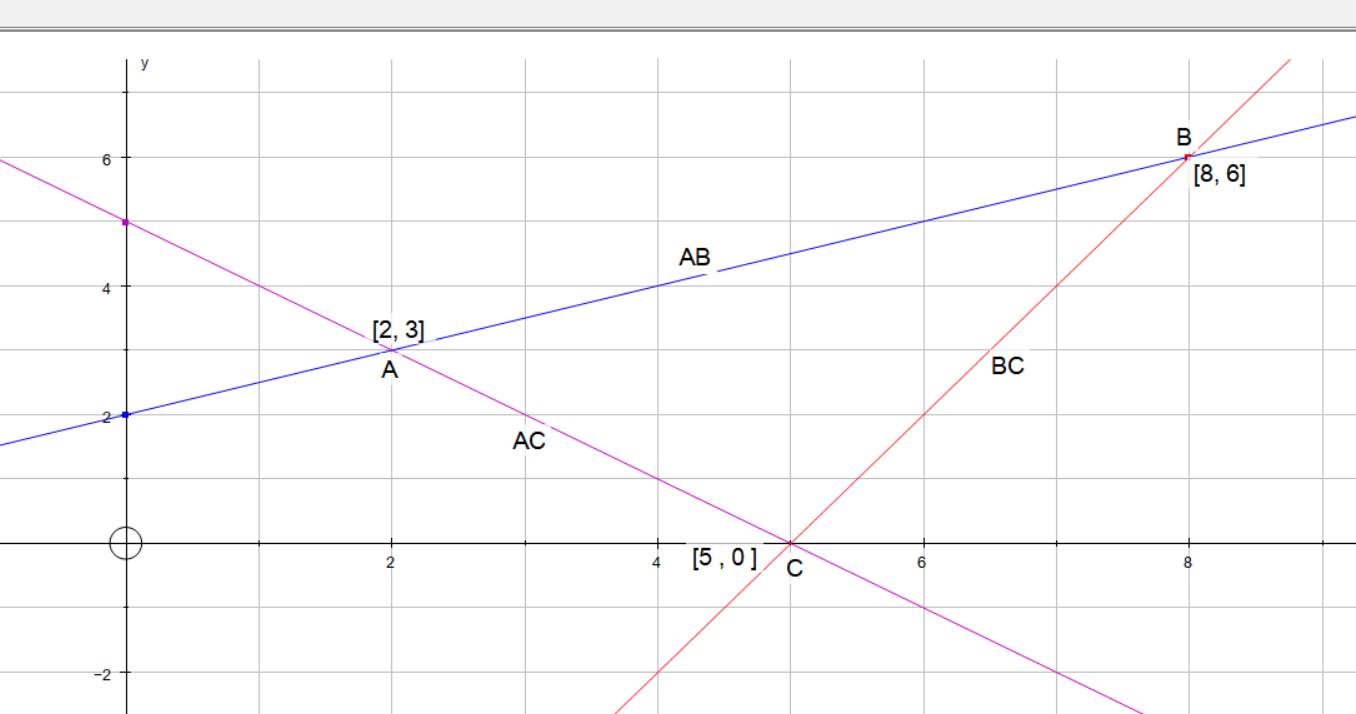
To find the coordinates of A B C, we need to find the intersection of the vector lines. This can be done equating each pair of vector lines.
To find point A we will use vector lines AB and AC. See diagram.
#AB =AC#
#((0),(2))+r((2),(1))=((0),(5))+t((1),(-1))#
#color(white)(->)2r=t#
#2+r=5-t#
Solving for #r# and #t#:
#r=3-t#
#2(3-t)=t=>t=2#
#2r=2=>r=1#
Using these in #AB =AC#
#((0),(2))+1((2),(1))=((0),(5))+2((1),(-1))#
#((2),(3))=((2),(3))#
Coordinate of A: #color(white)(8)( 2 color(white)(1), 3 )#
To find point B we will use vector lines AB and BC.
#AB = BC#
#((0),(2))+r((2),(1))=((8),(6))+s((-1),(-2))#
#color(white)(888)2r=8-s#
#2+r=6-2s#
#r=4-2s#
#2(4-2s)=8-s=>s=0#
#2+r=6-2(0)=>r=4#
Using these in #AB =BC#
#((0),(2))+4((2),(1))=((8),(6))+0((-1),(-2))#
#((8),(6))=((8),(6))#
Coordinate of B: #color(white)(8)( 8 color(white)(1), 6 )#
To find point C we will use vector lines AC and BC.
#AC=BC#
#((0),(5))+t((1),(-1))=((8),(6))+s((-1),(-2))#
#color(white)(8888)t=8-s#
#5-t=6-2s#
#5-(8-s)=6-2s=>s=3#
#t=8-3=>t=5#
Using these in #AC =BC#
#((0),(5))+5((1),(-1))=((8),(6))+3((-1),(-2))#
#((5),(0))=((5),(0))#
Coordinate of C: #color(white)(8)( 5 color(white)(1), 0 )#
To calculate the lengths of the sides, we could either use the distance formula or find vectors #vec(AB), vec(AC) and vec(CB)# and find their magnitude.
Using vectors.
#vec(AB)=((8),(6))-((2),(3))=((6),(3))#
#vec(AC)=((5),(0))-((2),(3))=((3),(-3))#
#vec(CB)=((8),(6))-((5),(0))=((3),(6))#
#||AB||=sqrt((6^2)+(3^2))=sqrt(45)=3sqrt(5)#
#||AC||=sqrt((3^2)+(-3^2))=sqrt(18)=3sqrt(2)#
#||CB||=sqrt((3^2)+(6^2))=sqrt(45)=3sqrt(5)#
Sides AB and BC are of equal length.
Coordinates:
#A=(2 , 3)#
#B=( 8 , 6 )#
#C=( 5 ,0 )#
Side lengths:
#AB=3sqrt(5)#
#BC=3sqrt(5)#
#AC=3sqrt(2)#



