For what values of x, if any, does #f(x) = 1/(e^x-3x) # have vertical asymptotes?
1 Answer
May 20, 2016
See below.
Explanation:
So in general, vertical asymptotes occur when the denominator in the function is zero, such that it's value doesn't exist,
Therefore, we need
As it turns out, this is really quite hard to solve. I would use a graphical calculator or app to solve this.
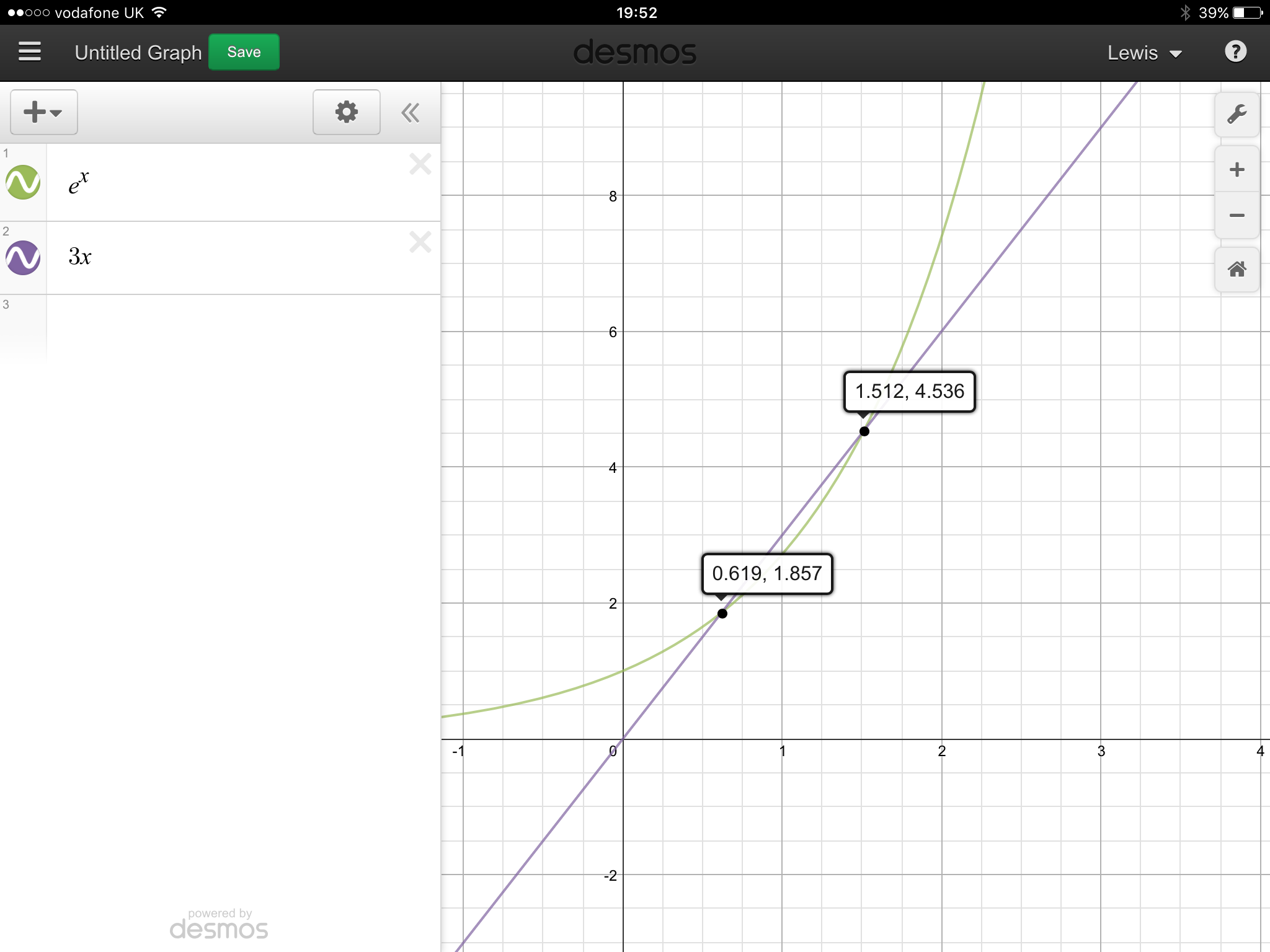
But if we want to find solutions analytically then we could use the Taylor expansion for

