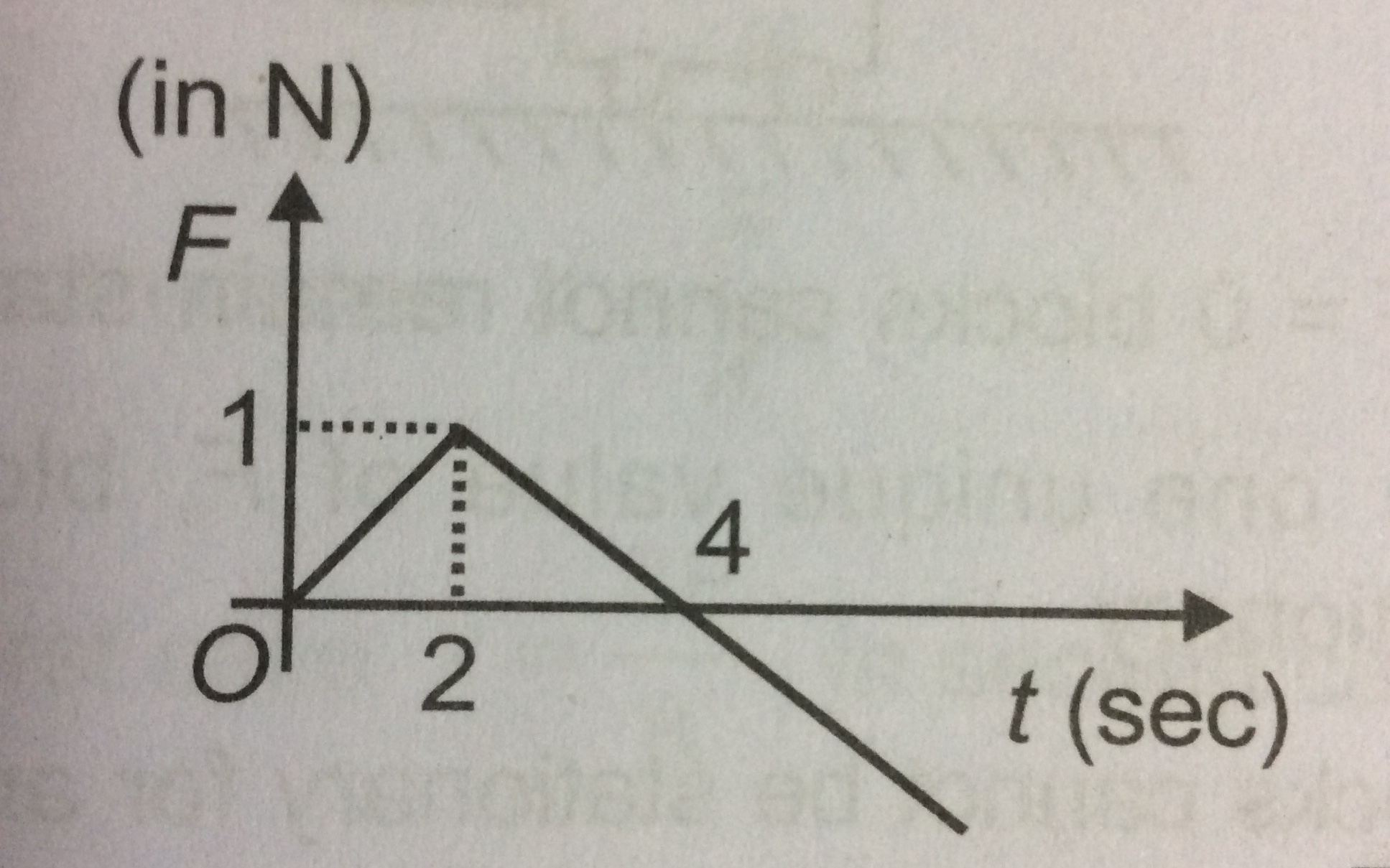
Force acting on a body varies with time as shown below. If the initial momentum of the body is #vecP# then the time taken by the body to retain its momentum #vecP# again is?

Question

17957 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-08-16T15:56:45

This is what I get.

For #t=0# to #t=2#, Force equation can be written in the standard form

#y=mx+c#
#vecF_1(t)=t/2#

Let #m# be mass of body. From Newton's second Law of motion.
#vec a(t)=1/mxxt/2#

Acceleration #veca-=(dvecv)/dt#
#:. vecv(t)=1/(m) int t/2dt#
#=>vecv(t)=1/m ( t^2/4+C)#
where #C# is constant of integration.

At #t=0#, #vecv(t)=vecp/m#
#=>vecp/m=C#
#vecv(t)=1/m ( t^2/4+vecp)# .....(1)

Velocity at #t=2# is found as
#vecv(2)=1/m(1+vecp)# ......(2)

Force equation for #t=2# and thereafter becomes

#vecF_2(t)=-1/2t+2#
#veca_2(t)=-1/m(t/2-2)#
#vecv_2(t)=-1/m int(t/2-2)dt#
#vecv_2(t)=-1/m ( t^2/4-2t+C_1)#
where #C_1# is constant of integration

Using (2) to find out #C_1#

#vecv_2(2)=-1/m (-3+C_1)=1/m(1+vecp)#
#=> (-3+C_1)=-1-vecp#
#=>C_1=2-vecp#

#:. vecv_2(t)=-1/m(t^2/4-2t+2-vecp)# ......(3)

Imposing the given condition and solving for #t#

#-vecp=t^2/4-2t+2-vecp#
#t^2-8t+8=0#

Solution of the quadratic gives us

#t=(8+-sqrt(64-4xx1xx8))/2#
#t=4+-2sqrt2#

Taking only #-ve# sign for original question.
For magnitude of momentum we have two solutions as above.