Four holes of radius R are cut from a thin square plate of the side 4R and mass M in XY plane as shown. Then moment of inertia of the remaining portion about z-axis is=? Plz explain clearly!!
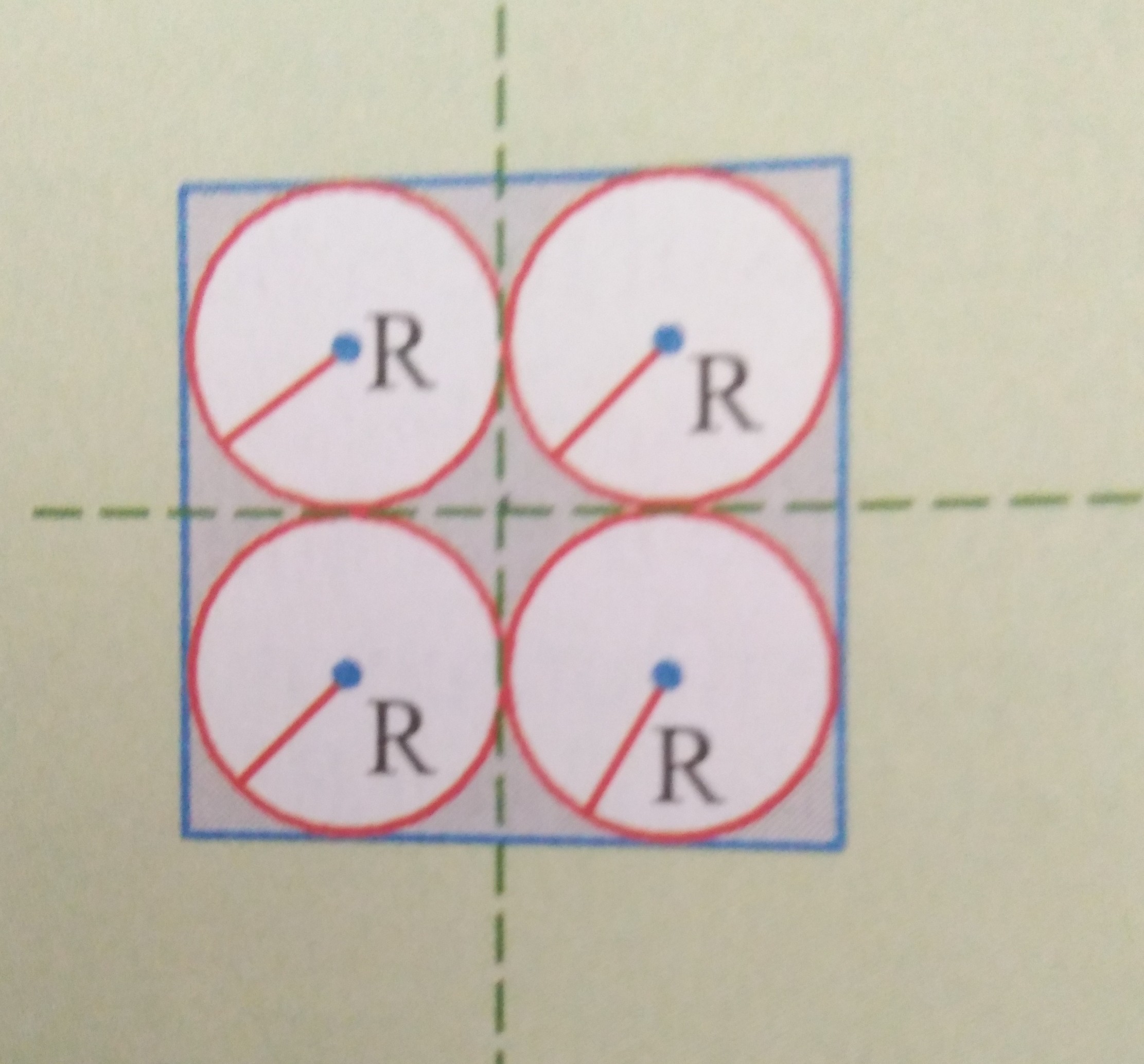
1 Answer
Apr 12, 2018
Explanation:
For the
# I_(zz)=1/12 m (h^2+w^2) #
That's for rotation around an axis perpendicular to it's centre.
The plate has density
A single disc, therefore, has mass:
A disc's inertia about it's centre is therefore:
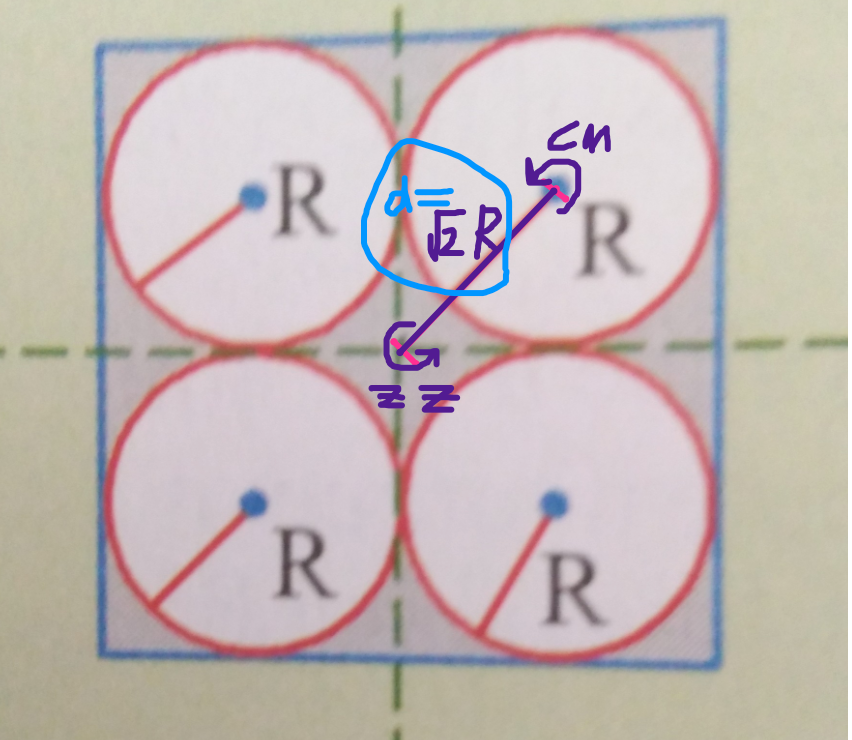
Using the parallel axis theorem (see drawing):
So the inertia of the hollowed out plate is:

