Gallium consists of 2 isotopes. One of those isotopes is 71-Ga with a mass of 70.92amu with an abundance of 39.892%. What is the mass number of the other isotope?
1 Answer
Explanation:
At first glance, it may seem like the problem didn't provide you with enough information.
However, if you have access to a periodic table, you can determine the mass number of the second isotope by examining its atomic mass.
So, the key to this problem is the fact that gallium has two isotopes. This means that the percent abundances of these two isotopes must amount to
This means that the percent abundance of the second isotope will be equal to
#100% - 38.892% = 61.108%#
Now, pull up your periodic table and look for gallium,
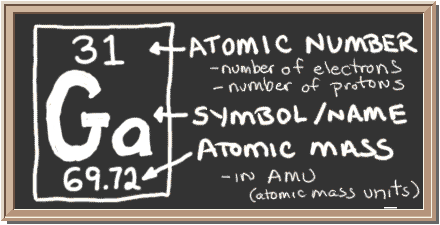
Notice that gallium has an atomic mass of
#color(blue)("relative atomic mass" = sum_i ("isotope"_i xx "abundance"_i))#
This means that the weighted average of the atomic masses of its two isotopes must be equal to
#"70.92 u" xx 0.38892 + color(blue)(x) xx 0.61108 = "69.72 u"#
Here
Solve this equation for
#color(blue)(n) = ("69.72 u" - "70.92 u" xx 0.38892)/0.61108 = "68.956 u"#
Now that you know the second isotope's atomic mass, you can find its mass number, which represents the number of protons and neutrons the isotope contains in its nucleus, by rounding this value to the nearest whole number.
In your case, the mass number of this second isotope will be
#68.956 -> color(green)(69)#

