Gauss' Law?
Figure shows a point charge q = 126μC at the center of a spherical cavity of radius
3.66cm in a piece of metal. Use Gauss’ law to find the electric field (a) at point P1, halfway from
the center to the surface, (b) at point P2.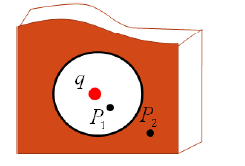
Figure shows a point charge q = 126μC at the center of a spherical cavity of radius
3.66cm in a piece of metal. Use Gauss’ law to find the electric field (a) at point P1, halfway from
the center to the surface, (b) at point P2.
1 Answer
Explanation:
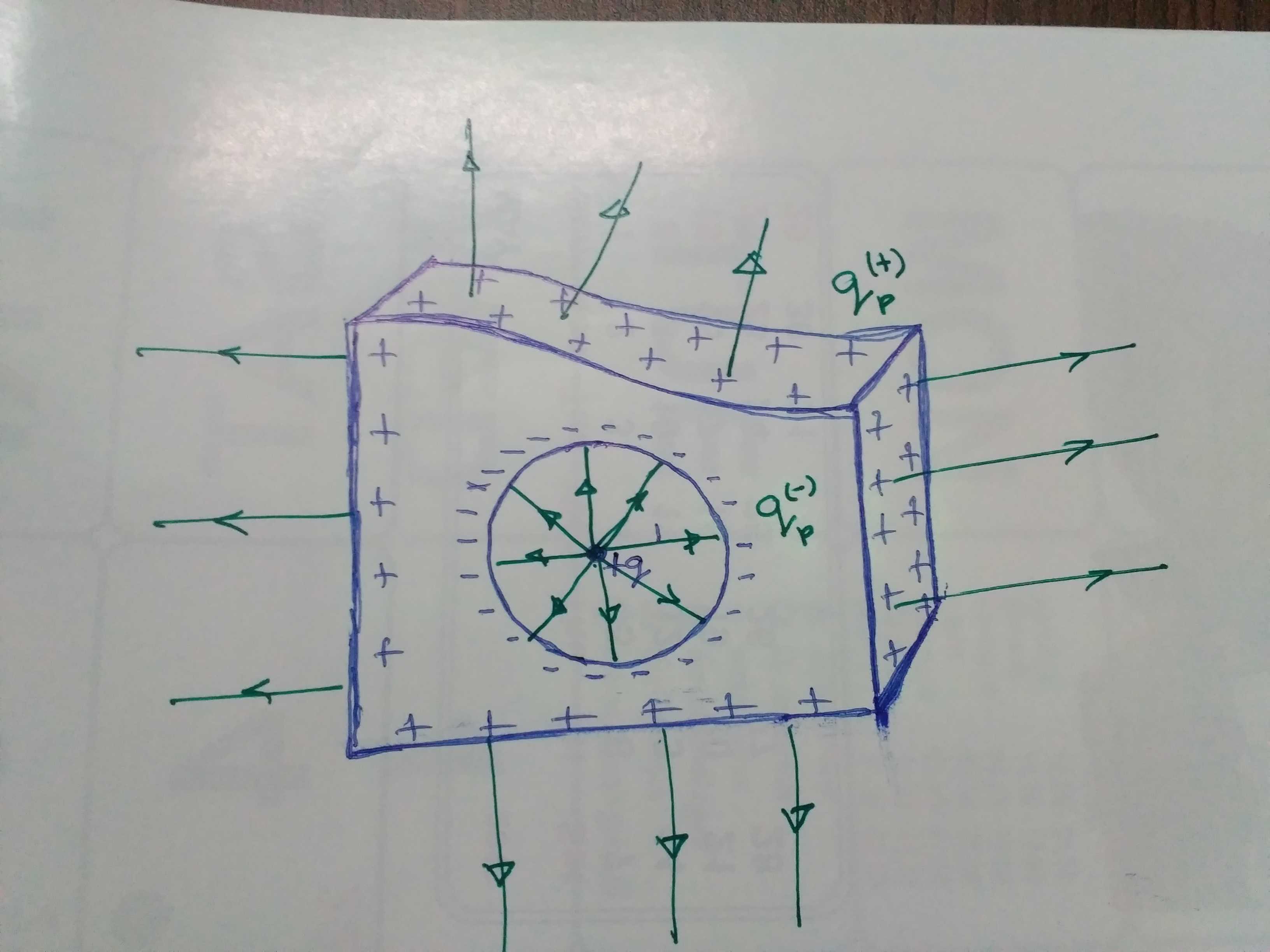
The electric field inside a good conductor cannot be non-zero. If the electric field has to vanish inside a conductor, it must get polarized such that
But since the conductor is electrically neutral, each of these negative polar charges will have a positive charge of same magnitude associated with them. These would have drifted to the surface of the good conductor. The electric field will continue outside the conductor originating from these outer
Interior: Let
By Gauss's law the electric flux through this surface is -
The electric field is spherically symmetric and so will have the same magnitude (
Exterior: Point
If we imagine a gaussian sphere centered on the central charge such that point
Therefore,

