Geometry is fun or ducks do not like water. Is this conjunction, disjunction, negation, or conditional?
1 Answer
This is a disjunction:
Geometry is fun
#" "# or#" "# ducks do not like water.
Explanation:
This is a disjunction of two clauses: "geometry is fun" and "ducks do not like water". The central connective word is "or".
It is approximately logically equivalent to the conditional statement:
If ducks like water then geometry is fun.
We can break it down into parts as follows:
-
Let
#G# be the statement "geometry is fun". -
Let
#D# be the statement "ducks like water".
Then the given statement can be represented symbolically as:
#G vv not D" "# "G or not D"
The statement "If ducks like water then geometry is fun." would be represented as:
#D -> G" "# "D implies G"
These two statements are equivalent in Boolean logic.
We can draw a Venn diagram looking like this:
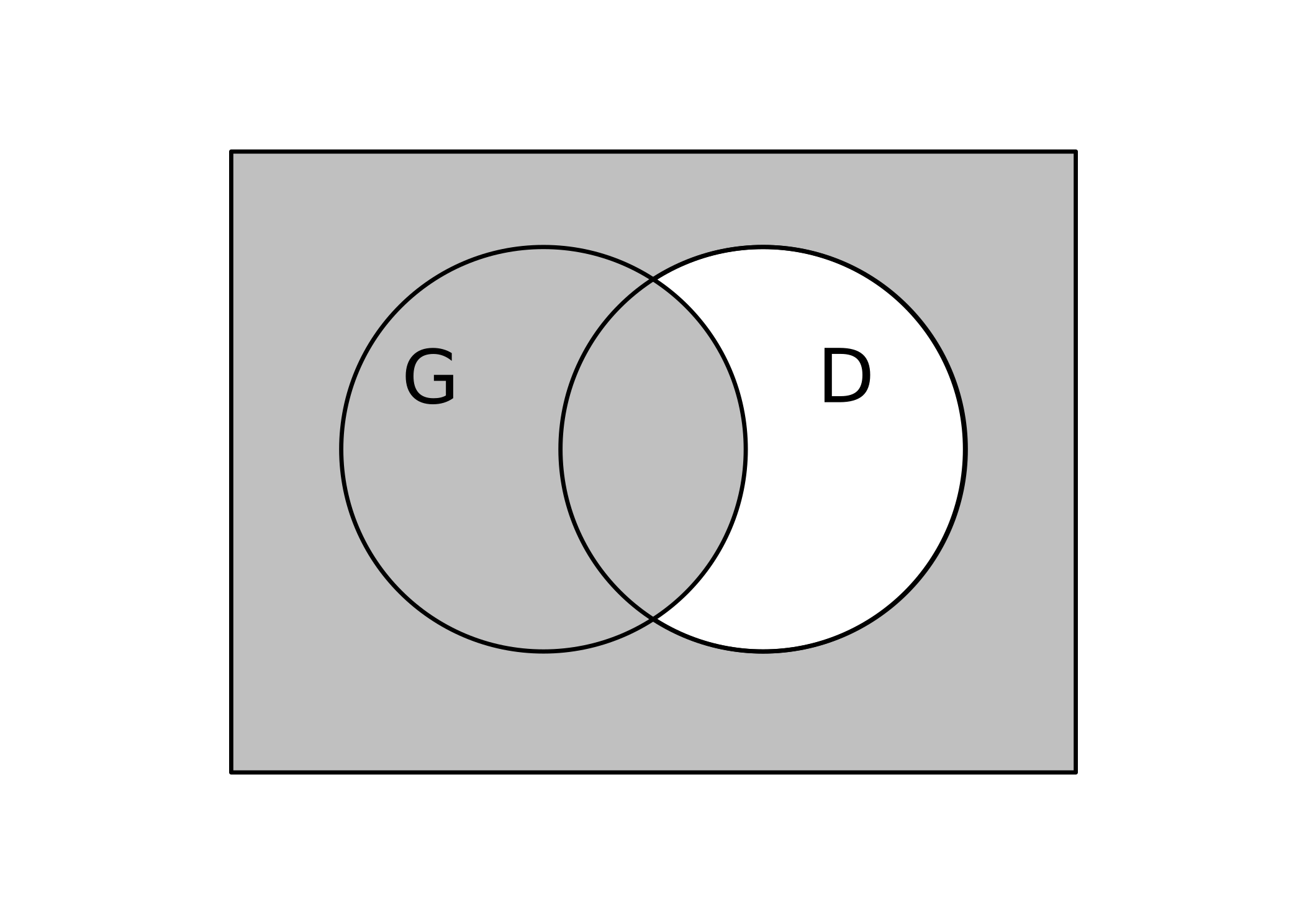
The left hand circle represents the proposition "geometry is fun" and the right hand circle the proposition "ducks like water".
The shaded region corresponds to both the statements:
#G vv not D" "# "Geometry is fun or ducks do not like water."
#D -> G" "# "If ducks like water then geometry is fun."
However, I think that it is important to note that natural language and meaning are more subtle than Boolean logic. So it would be inaccurate to classify the given statement as a conditional.

