Question

Gibbs Free Energy. Why are equilibrium constants for a chemical reaction temperature dependent?

Answer 1

Because rate constants are temperature-dependent, and by changing the temperature, you change the ratio of rate constants so that `K -= k_(fwd)/k_(rev)` changes.

---

Although you may be familiar with this in the context of this equation:

`DeltaG^@ = -RTlnK`

That isn't actually where the temperature dependence is readily seen. Consider the Arrhenius equation:

`k = Ae^(-E_a//RT)`

where `k` is the rate constant at temperature `T`, `A` is the frequency factor of the reaction (i.e. the limiting rate constant at high temperature), and `E_a` is the activation energy.

Now, take two temperatures and two rate constants, assuming `A` remains constant:

`k_2/k_1 = "exp"(-E_a/R[1/T_2 - 1/T_1])`

`=> color(green)(ln(k_2/k_1) = -E_a/R[1/T_2 - 1/T_1])`

where `"exp"(x) = e^x`.

We currently have the relationship for two rate constants each at different temperatures. Now, think about where activation energy is on a reaction coordinate diagram:

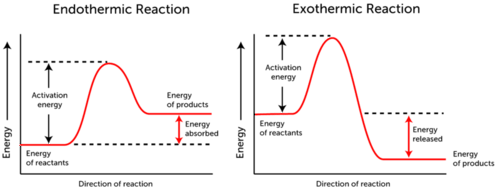
We see that `E_(a,fwd)` is the energy from reactant to transition state for the forward reaction, and `E_(a,rev)` is the energy from product to transition state for the reverse reaction.

So now, consider that the rate of the forward reaction equals the rate of the reverse reaction at equilibrium. Take the reaction as:

`aA + bB rightleftharpoons cC + dD`

The rate laws would be:

`r_(fwd)(t) = k_(fwd)[A]^a[B]^b`
`r_(rev)(t) = k_(rev)[C]^c[D]^d`

So we set them equal:

`k_(fwd)[A]^a[B]^b = k_(rev)[C]^c[D]^d`

By definition, the equilibrium constant is:

`=> K -= ([C]^c[D]^d)/([A]^a[B]^b) = (k_(fwd))/(k_(rev))`

Now, take `K` at different temperatures, so that:

`K_1 = (k_(1,fwd))/(k_(1,rev))` `" "" "` `K_2 = (k_(2,fwd))/(k_(2,rev))`

Substitute back into the Arrhenius equation for the forward and reverse reactions.

`ln(k_(2,fwd)/k_(1,fwd)) = -E_(a,fwd)/R[1/T_2 - 1/T_1]`

`ln(k_(2,rev)/k_(1,rev)) = -E_(a,rev)/R[1/T_2 - 1/T_1]`

Use the fact that `K_i = (k_(i,fwd))/(k_(i,rev))` to see that by subtracting these equations we proceed to get the left-hand side to be:

`ln(k_(2,fwd)/k_(1,fwd)) - ln(k_(2,rev)/k_(1,rev))`

`= ln(k_(2,fwd)/k_(1,fwd) cdot 1/(k_(2,rev)//k_(1,rev)))`

`= ln((k_(2,fwd)//k_(2,rev)) / (k_(1,rev)//k_(1,fwd)))`

`= ln(K_2/K_1)`

The right-hand side by subtraction becomes:

`-E_(a,fwd)/R[1/T_2 - 1/T_1] - (-E_(a,rev)/R[1/T_2 - 1/T_1])`

`= -(E_(a,fwd) - E_(a,rev))/R[1/T_2 - 1/T_1]`

But look up at the reaction coordinate diagram above. We can make the connection that `color(green)(E_(a,fwd) - E_(a,rev) = DeltaH_(rxn))`.

Therefore, we arrive at the van't Hoff equation for equilibrium constants vs. temperature:

`color(blue)(ln(K_2/K_1) = -(DeltaH_(rxn))/R[1/T_2 - 1/T_1])`

which looks strikingly like the Arrhenius equation (not a coincidence!).

Or put in another form,

`color(blue)(ln K = -(DeltaH_(rxn))/R 1/T + (DeltaS_(rxn))/R)`

Hence, we have shown that equilibrium constants certainly are temperature-dependent.

Endothermic reactions have increased `K` at higher temperatures, and exothermic reactions have decreased `K` at lower temperatures.