Question

Give an example of a function which is one to one but not onto,with reason.?

Answer 1

`f(x) = e^x`

Explanation:

in an 'onto' function, every `x`-value is mapped to a `y-`value.

in a one-to-one function, every `y`-value is mapped to at most one `x`- value.

this means that in a one-to-one function, not every `x`-value in the domain must be mapped on the graph. it only means that no `y`-value can be mapped twice.

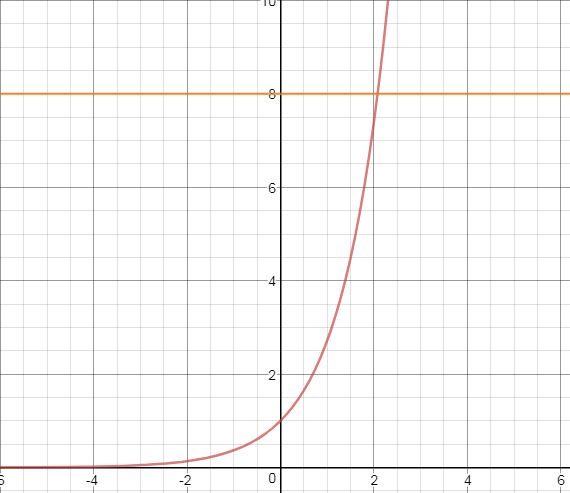
the graph of `e^x` is one-to-one.

there is no more than one `x`-value for each `y`-value, and there is no more than one `y`-value for each `x`-value.

this can be shown using the horizontal line test: a horizontal line, drawn anywhere on the graph (i.e. of any `y`-value), will not intersect with a one-to-one function more than once (if at all).

the graph of `e^x` is not surjective.

not every `y`-value is mapped on the graph; `e^x` can never be `0` or below. `y=0` is the horizontal asymptote of the graph.