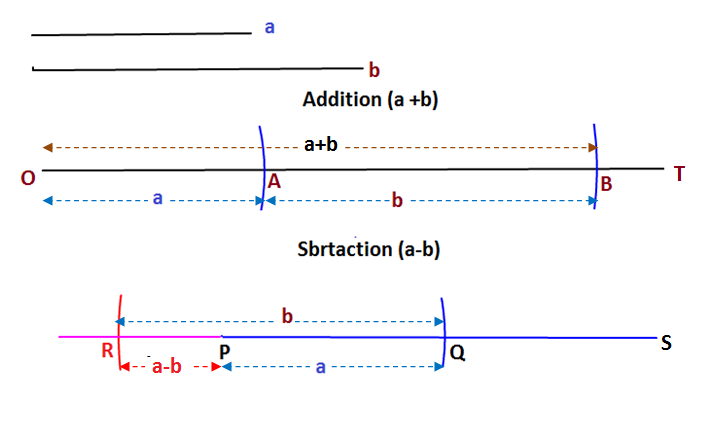
Addition and subtraction of two numbers #a and b# are made by geometric construction using only a straight edge and compass as shown above.
For addition a long line OT is first drawn using ruler then two line segments #OA=a# and #AB=b# are cut off from it one after another with the help of a compass. The measure of the line segment #OB# will represent the sum of two numbers #a and b#
In case of subtraction one line segment #PQ=a# is first cut off from long line PS and subsequently #QR =b# is cut off in reverse direction from QP or extended QP (if necessary when a < b). The line segment #PR# will represent the result of subtraction.
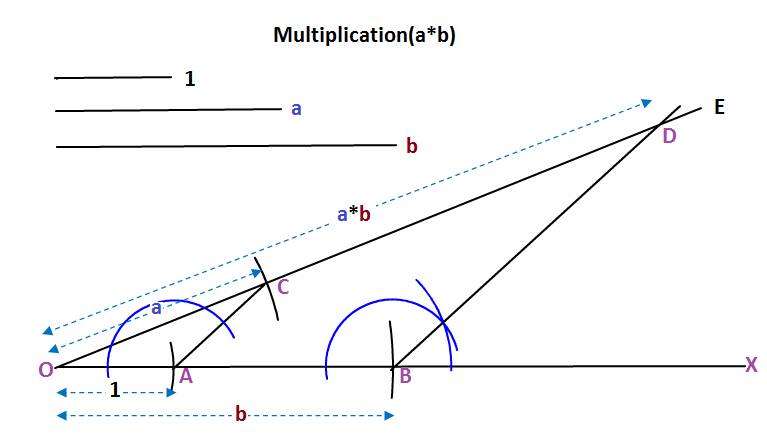
Multiplication by geometric method is explained in above figure.
Here three line segments are taken. One represents unit length and other two represent two numbers #a and b# on the basis of unit length,
From a line segment QX , #OA=1and OB=b# are cut off. An acute angle #/_EOX# is drawn. The line segment #OC=a# is cut off from OE. #A andC# are joined. A line BD parallel to AC is drawn from B, which intersects OE at D. Now #OD# will represent #a"*"b#
Proof
#Delta OAC and Delta OBD# are similar as #AC"||"BD#
So #(OD)/(OC)=(OB)/(OA)#
#=>(OD)/a=b/1#
#=>OD=axxb#
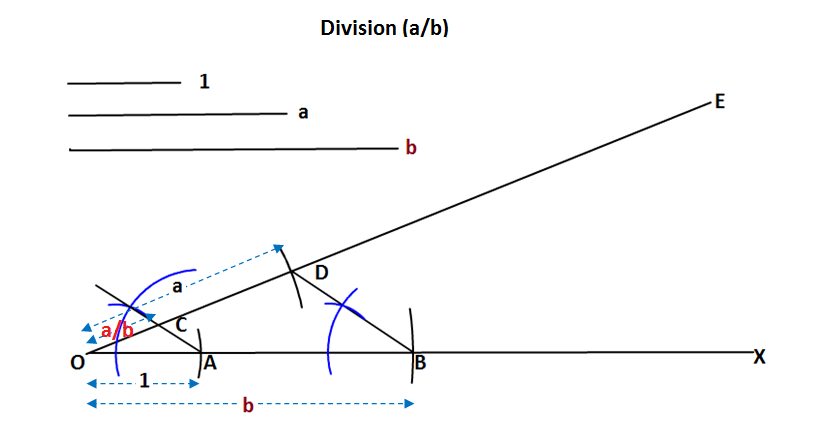
Division by geometric method is explained in above figure.
Here three line segments are taken. One represents unit length and other two represent two numbers #a and b# with respect to the unit length,
From a line segment QX , #OA=1and OB=b# are cut off. An acute angle #/_EOX# is drawn. The line segment #OD=a# is cut off from OE. #BandD# are joined. A line AC parallel to BD is drawn from A, which intersects OE at C. Now #OC# will represent #a/b#
Proof
#Delta OAC and Delta OBD# are similar as #AC"||"BD#
So #(OC)/(OD)=(OA)/(OB)#
#=>(OC)/a=1/b#
#=>OC=a/b#




