Given #C_1->y^2+x^2-4x-6y+9=0#, #C_2->y^2+x^2+10x-16y+85=0# and #L_1->x+2y+15=0#, determine #C->(x-x_0)^2+(y-y_0)^2-r^2=0# tangent to #C_1,C_2# and #L_1#?
1 Answer
There are two solutions as explained below.
Explanation:
Firstly we will represent the geometric objects in a more convenient formulation.
So
After reduction, we have
Now, given
find
such that
Here
We can stablish the following retationships
if
where
Finally we get the following equations
so we have four equations and four incognitas
Solving we obtain
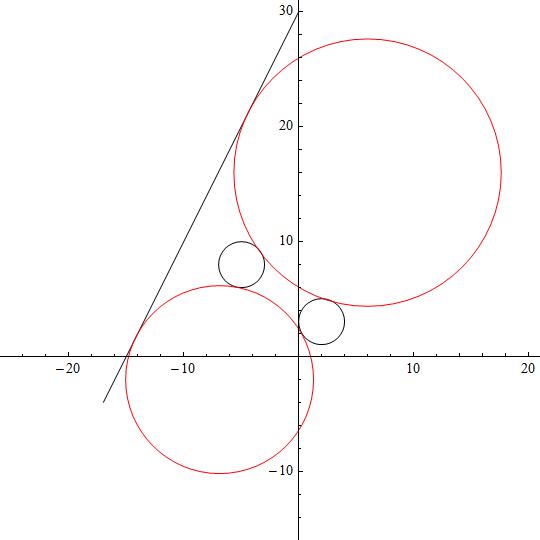
Attached the figure with the solutions in red and the initial geometric elements in black.