.
#f(x)=e^(-x)sinx#, #(-pi <= x <= pi)#
We set #y=0# to find the #x#-intercept(s):
#e^(-x)sinx=0#
#e^(-x)=0, :. 1/e^x=0, :. e^x=oo, :. x=oo#, This is outside our interval.
#sinx=0, :. x=-pi, 0, pi#
We set #x=0# to find the #y#-intercept(s):
#y=e^(-0)sin0=0#
Let's graph the function:
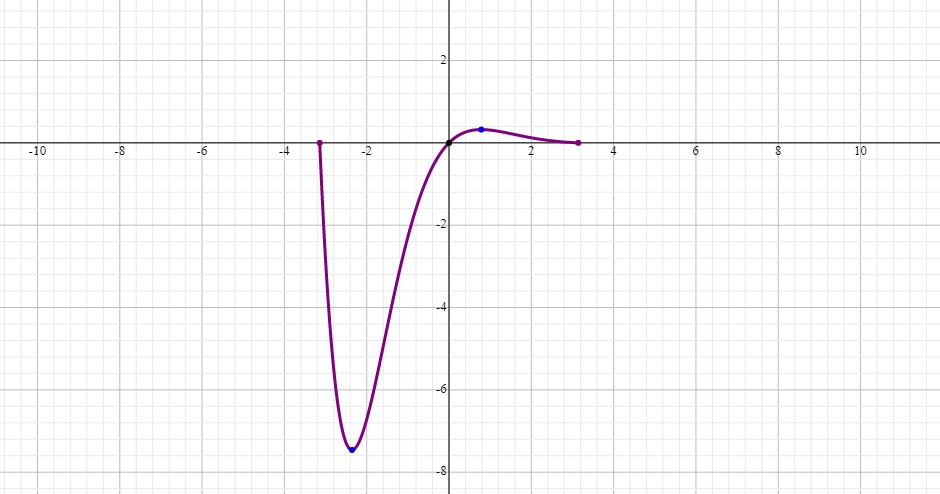
As can be seen, the #x# and #y# intercepts are verified.
To find the local extrema, we need to take the first derivative of the function and set it equal to #0#. Since our function is the product of two other functions, we use the product rule:
#dy/dx=e^(-x)cosx+(-e^(-x)sinx)=e^(-x)cosx-e^(-x)sinx#
#e^(-x)cosx-e^(-x)sinx=0#
#e^(-x)(cosx-sinx)=0#
#e^(-x)=0, :. 1/e^x=0, :. e^x=oo, :. x=oo#, This is outside our interval.
#cosx-sinx=0#
#cosx=sinx#
We divide both sides by #cosx#:
#tanx=1, :. x=arctan(1), :. x=pi/4, (-3pi)/4#
Without looking at the graph, we would have to conduct a first derivative test by trying values of #x# to the left and right of #pi/4# and #(-3pi)/4# to determine where the function is decreasing and increasing. This would tell us which of the extrema solutions is a local minimum and which is a local maximum.
But the graph shows us clearly that #x=(-3pi)/4# is the minimum and #x=pi/4# is the maximum. We now plug each of them into the function to find their #y#-coordinates:
#x=-(3pi)/4, :. y=e^(-(-(3pi)/4))sin(-(3pi)/4)=e^((3pi)/4)sin(-(3pi)/4)=10.55(-sqrt2/2)=-7.46#
#x=pi/4, :. y=e^(-pi/4)sin(pi/4)=0.46(sqrt2/2)=0.33#
Local Minimum #(-2.36, -7.46)#
Local Maximum #(0.79, 0.33)#
To find the inflection point(s), we need to take the second derivative of the function and set it equal to #0#:
#(d^2y)/dx^2=-e^(-x)sinx+(-e^(-x)cosx)-[(e^(-x)cosx+(-e^(-x)sinx)]#
#(d^2y)/dx^2=-e^(-x)sinx-e^(-x)cosx-e^(-x)cosx+e^(-x)sinx#
#(d^2y)/dx^2=cancelcolor(red)(-e^(-x)sinx)-e^(-x)cosx-e^(-x)cosxcancelcolor(red)(+e^(-x)sinx)#
#(d^2y)/dx^2=-2e^(-x)cosx#
#-2e^(-x)cosx=0#
#e^(-x)=0, :. 1/e^x=0, :. e^x=oo, :. x=oo#, This is outside our interval.
#cosx=0, :. x=pi/2, -pi/2#
These are the #x#-coordinates of the two inflection points. We will plug them into the function to get their #y#-coordinates:
#x=-pi/2, :. y=e^(-(-pi/2))sin(-pi/2)=e^(pi/2)sin(-pi/2)=4.81(-1)=-4.81#
#x=pi/2, :. y=e^(-pi/2)sin(pi/2)=0.21(1)=0.21#
Inflection Point-1, #(-1.57,-4.81)#
Inflection Point-2, #(1.57,0.21)#
The two extrema and two inflection points are verified on our graph.


