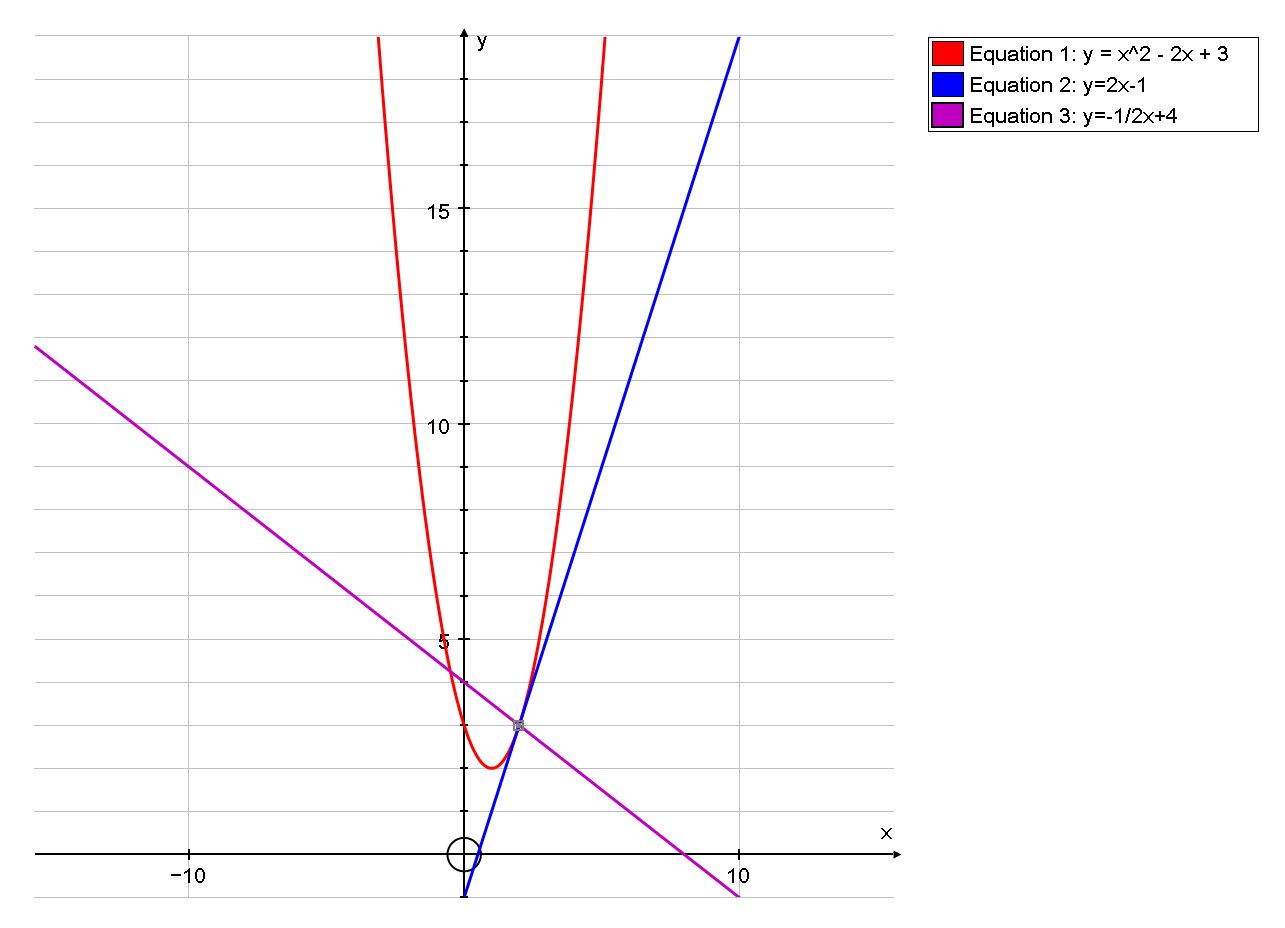
Given the parabola #y = x^2 - 2x + 3# how do you find the equation for the line which contains the point (2,3) and is perpendicular to the line tangents to the parabola at (2,3)?

Question

4943 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-11-05T00:26:29

# y=-1/2x+4 #

We have, # y = x^2 - 2x + 3 #

To get the gradient of the tangent at any particular point we need the first derivative:

So, # dy/dx = 2x-2 #

The tangent at #(2,3)# will have the gradient given by #dy/dx# with #x=2#

# x=2 => dy/dx=(2)(2)-2 = 2 #

Therefore, The tangent to the parabola at #(2.3)# has gradient #2#

The line that we seek is perpendicular to this tangent, and so the product of their gradients will be #-1#

ie, The line will have gradient #-1/2#

Using # y-y_1=m(x-x_1) # the equation of this line is given by:

# y-3=-1/2(x-2) #
# :. y-3=-1/2x+1 #
# :. y=-1/2x+4 #

enter image source here