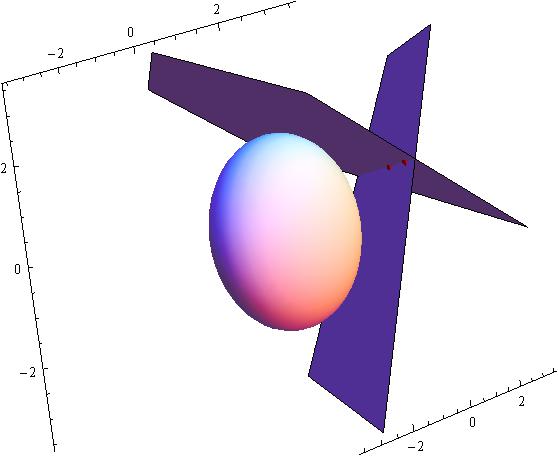
Calling
#Sigma->f(x,y,z)=y^2 + 3 x^2 + z^2 - 4=0#
and considering #p = (x,y,z)# such that
#p in Sigma#, we have
#vec n = (p-p_1) xx (p-p_2)# is a vector normal to the plane
#Pi# defined by the points #p, p_1, p_2#
Now, the vector #vec n# can be computed over #Sigma# as #grad f = ((partial f)/(partial x), (partial f)/(partial y), (partial f)/(partial z)) =2(3x,y,z) #
The #Sigma# tangent point is then determined by the equations
#{
(n_x/norm(vec n)=pmf_x/norm(grad f)),
(<< grad f, p_1-p_2 >> = 0),
(f(x,y,z)=0)
:}#(1)
or
#{((1 - z)/sqrt[(x + y-3)^2 + 2 (z-1)^2] pm (3 x)/sqrt[
9 x^2 + y^2 + z^2]=0),(y-3x=0),(y^2 + 3 x^2 + z^2 - 4=0):}#(2)
Solving for #x,y,z# we obtain
#p_(t_1) = (0.531359, 1.59408, -0.782233)# and
#p_(t_2) = (0.242834, 0.728503, 1.81449)# the tangency points
and also
#(grad _1 f)/norm(grad_1 f) =(vec n_1)/norm(vec n_1) = (0.668034, 0.668034, -0.327812) #
#(grad_2 f)/norm(grad_2 f) =(vec n_2)/norm(vec n_2)=-(0.349138, 0.349138, 0.869601)#
the corresponding normal surface vectors.
Note:
a) In (1,2) we consider only a vector component. The choice is one of
#(((1 - z)/sqrt[(x + y-3)^2 + 2 (z-1)^2] - (3 x)/sqrt[
9 x^2 + y^2 + z^2]),((1 - z)/sqrt[(x + y-3)^2 + 2 (z-1)^2] - y/sqrt[
9 x^2 + y^2 + z^2]),((x + y-3)/sqrt[(x + y-3)^2 + 2 (z-1)^2] - z/sqrt[
9 x^2 + y^2 + z^2]))#
b) The sign #pm# before the gradient is to qualify the two solutions to the problem.
c) Here #(cdot xx cdot)# represents the vector product and #<< cdot, cdot >># the scalar product. Also #norm(cdot)# represents the vector norm.