Given the system #{(x+y+z=a),(x^2+y^2+z^2=b^2),(xy=z^2):}# determine the conditions over #a,b# such that #x,y,z# are distinct positive numbers?
2 Answers
Explanation:
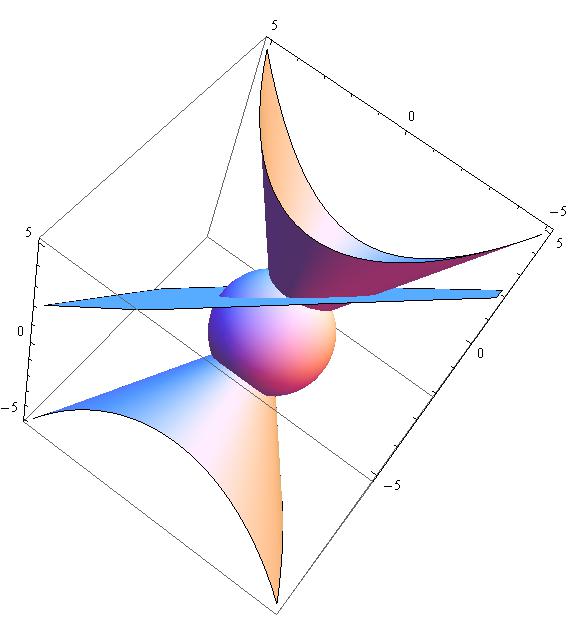
In the first octant (
triangular area, with vertices (a, 0, 0), (0, a, 0) and (0, 0, a). The
section of this area by the sphere
only if the length of the perpendicular from the origin on this plane
Consider the third as
hyperbolic cylinder. The part of this in
beyond the plane
For the hyperboloid to meet the section of the other two,
the length of the perpendicular from the origin O on this plane ( that
touches the hyperboloid ).,
Instead, for (c-absent)
Under this condition,
Despite that
surfaces, it is relevant that the section of
z=c is the RH
See below.
Explanation:
Substituting
so
but
Solving the polynomial
we have
Attached a figure showing the surfaces,