Question

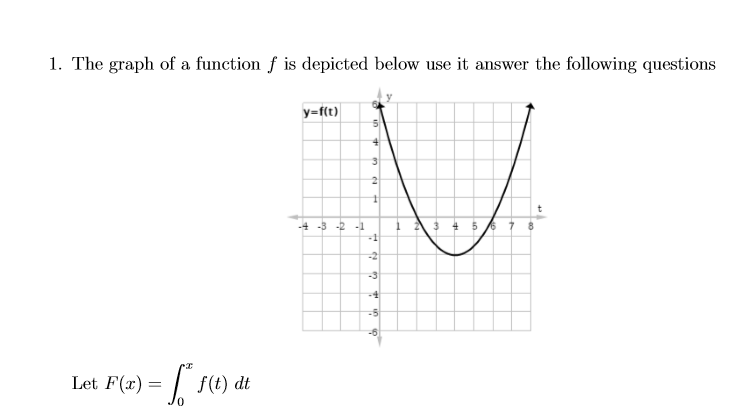
Given this graph of `f` where does `F` have a local min/max and find the intervals where `F` is concave up/down?

Answer 1

By the Fundamental Theorem of Calculus, `F'(x) = f(x)`.

Explanation:

So we are looking at a graph of the derivative of `F(x)`.

Where the derivative is positive, the graph of the derivative is above the `x` axis and `F` is increasing.
Where the derivative is negative, the graph of the derivative is below the `x` axis and `F` is decreasing.

So `F` has a relative maximum at `x=2` (where the derivative of `F` changes from + to -).
and `F` has a relative minimum at `x=6` (where the derivative of `F` changes from - to +).

(The graph of) `F` is concave up where `F''(x)` is positive and that happens where `F'(x)` is increasing. We can see on the graph that that happens for `x > 4`.

Dually, the graph of `F` is concave down where the derivative of `F` is decreasing. In this case, for `x < 4`.