Given two graphs of piecewise functions f(x) and g(x), how do you know whether f[g(x)] and g[f(x)] are continuous at 0?
1 Answer
Oct 17, 2015
There is no simple answer.
Explanation:
For
Find
Examine the graphs to find the one-sided limits,
If they are equal and are the same as
Examples
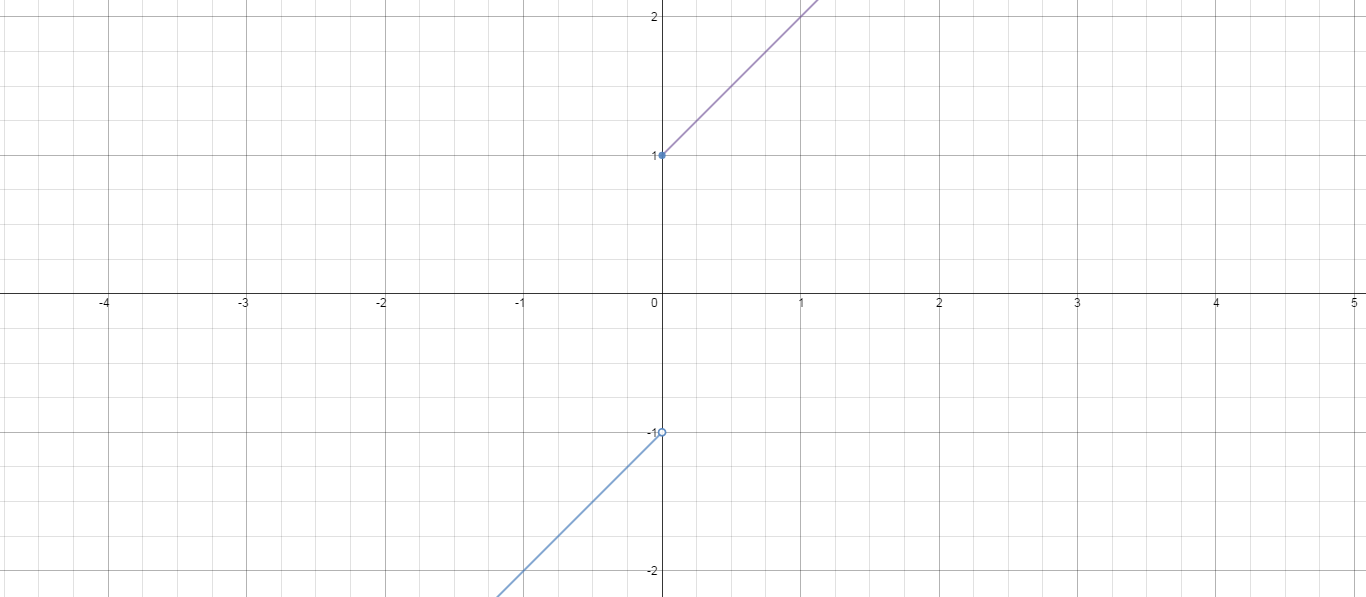
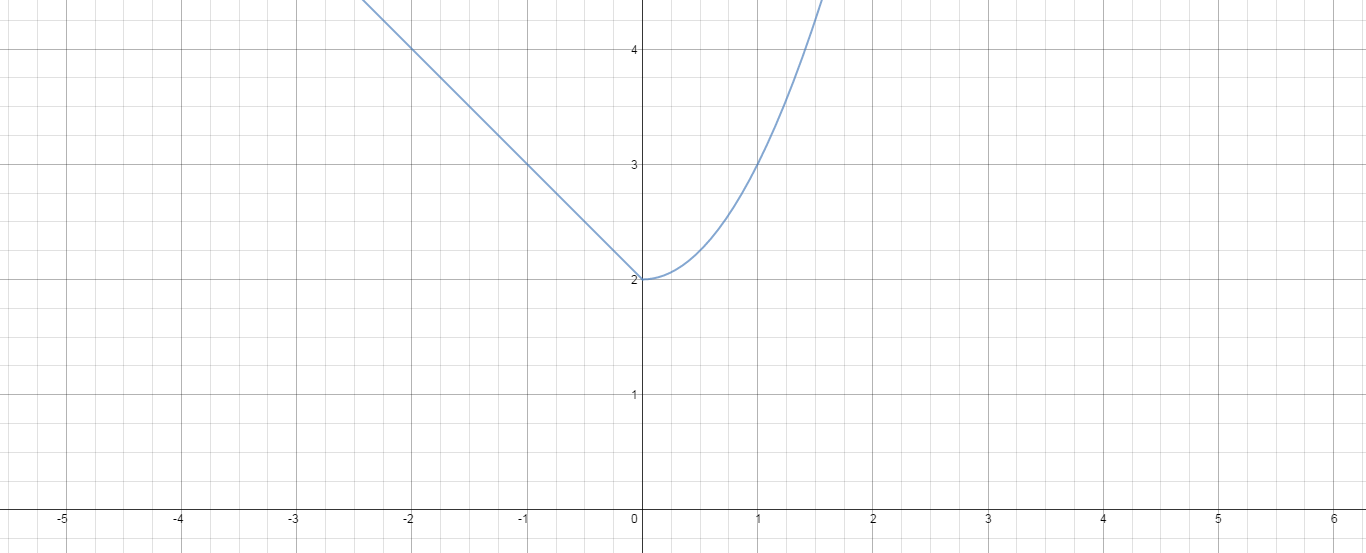
But for
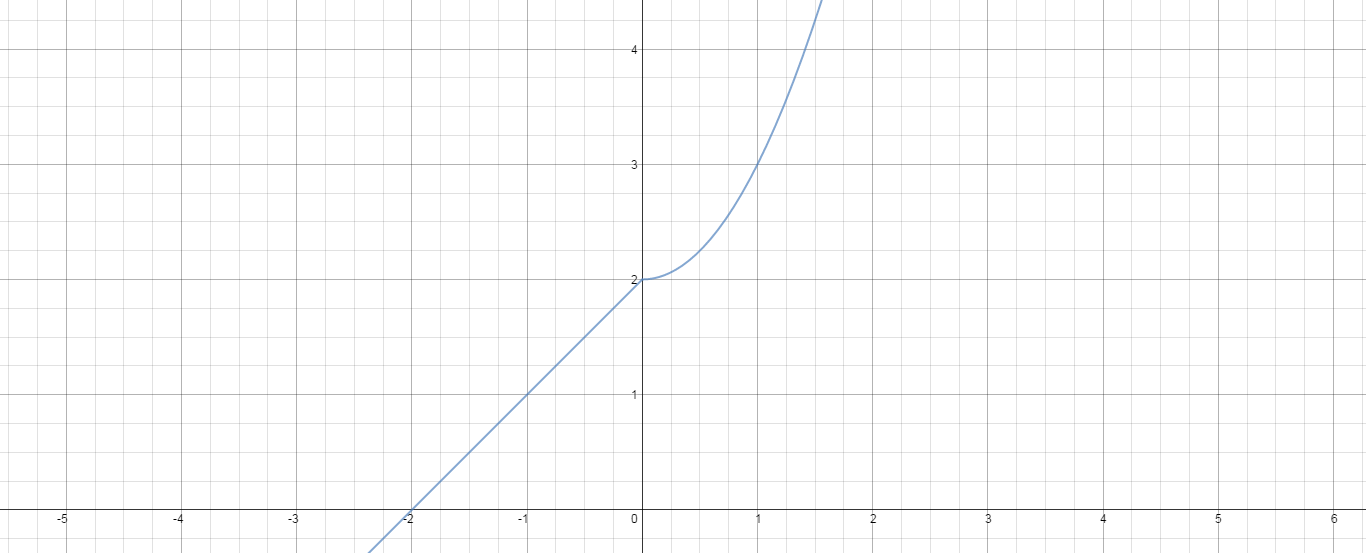
Here is another function I'll call
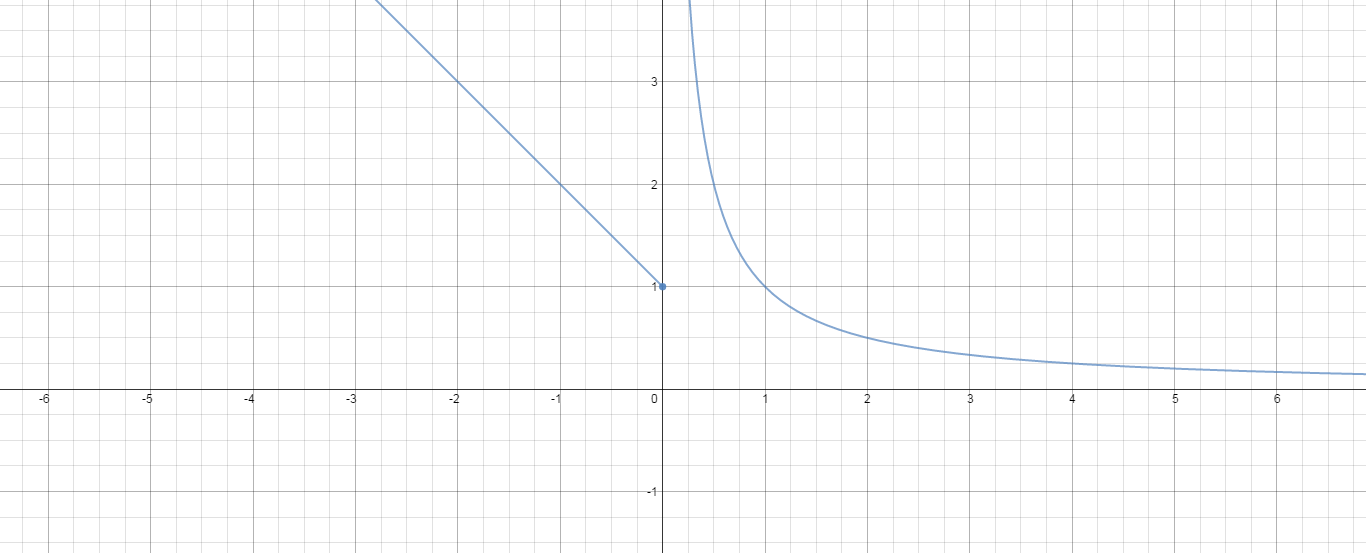
Neither
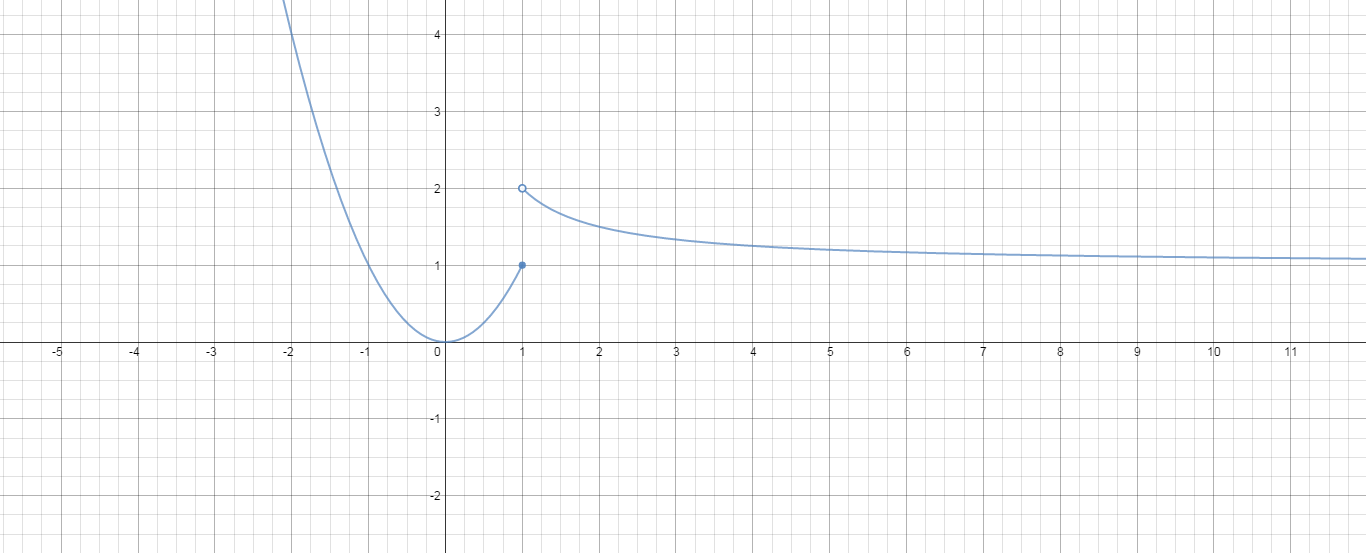
Perhaps someone else can summarize a method for this.

