Hello friends, please, I need to know how to get the answer out of this exponential equation? thank you

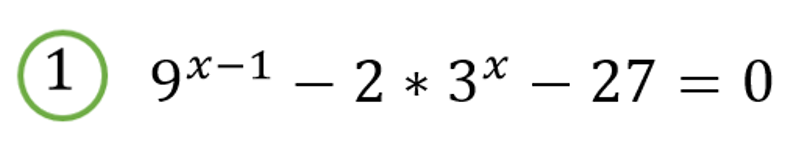
enter image source here

1 Answer
sente
Nov 5, 2016

#x = 3#

Explanation:

First, we will use the properties of exponents that

  • #a^(x+y) = a^xa^y#
  • #(a^x)^y = a^(xy) = (a^y)^x#

#9^(x-1) - 2*3^x-27 = 0#

#=> 9^(-1)*9^x - 2*3^x - 27 = 0#

#=> 1/9*(3^2)^x - 2*3^x - 27 = 0#

#=> 1/9*(3^x)^2 - 2*3^x - 27 = 0#

With these manipulations, we can see this has the form of a quadratic equation, but with #3^x# as the variable rather than just #x#. As such, we will apply the quadratic formula:

#3^x = (-(-2)+-sqrt((-2)^2-4(1/9)(-27)))/(2(1/9))#

#=(2+-sqrt(16))/(2/9)#

#=(2+-4)/(2/9)#

#=9+-18#

Note that #3^x > 0# for all real #x#. Thus the case in which #3^x = 9-18 = -9# has no real solutions. This leaves us with the case in which #3^x = 9+18#.

#3^x = 9+18#

#=> 3^x = 27#

#=> 3^x = 3^3#

The answer is pretty clear at this point, but we can justify it properly by using logarithms. We will use the following properties of logarithms:

  • #log(a^x) = xlog(a)#
  • #log_a(a) = 1#

With those, we have

#log_3(3^x) = log_3(3^3)#

#=> xlog_3(3) = 3log_3(3)#

#:. x = 3#

Finally, we can check our answer:

#9^(3-1) - 2*3^3-27 = 81 - 2*27 - 27 = 0#

as desired.

Related questions
See all questions in Applications of Exponential Functions
Impact of this question
1874 views around the world
You can reuse this answer
Creative Commons License