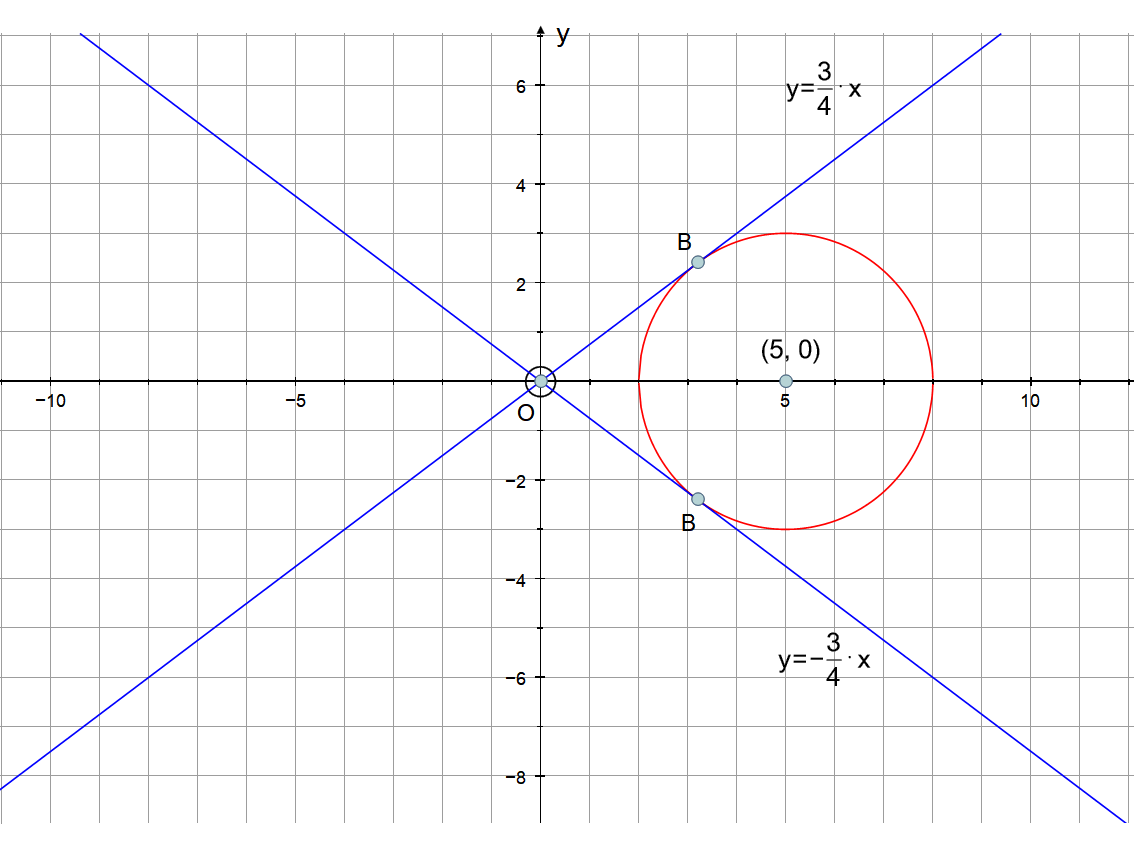
Help for circle geometry question?!
Line OB is a tangent to the circle whose equation is #(x-5)^2-y^2=9# . A is the centre of the circle. Find the general equation of line OB.
Line OB is a tangent to the circle whose equation is
1 Answer
Explanation:
I am assuming the equation of the circle should be:
If the line OB is tangent to the given circle it will have the form:
Substituting this in the equation of the circle:
Expanding:
Simplifying:
Arrange into the form
Because we are just touching the circle at one point we need the roots of this quadratic to be repeated i.e. discriminant = zero.
Discriminant is:
So our equations are:
There will always be two tangent lines that pass through a point outside the circle.
The general form of the tangent equation passing through the origin would be: