Question One:
In the annotated diagram below, we are given a right angle which you know is #90°# We are also given an angle of #47°#. Given this, we can say a few things that will help us find the values of #x# and #y#
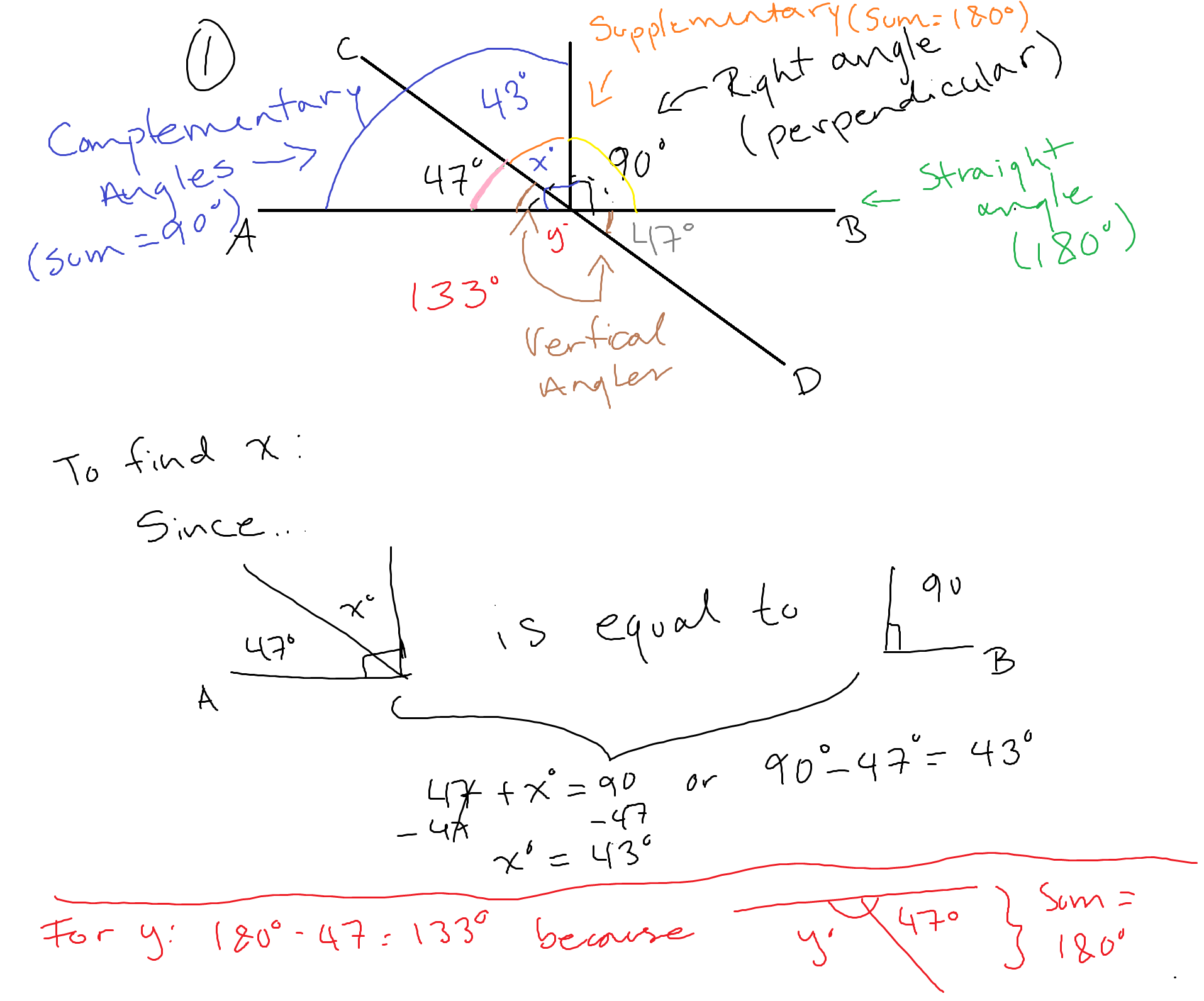
For #x#, we can see that we have a perpendicular angle with the right side already labeled for us, we can say that the right side is also #90°# which means that the line segment #bar(AB)# is equal to #180°# In addition, we have some complementary angles on the left whose sum of the angles is #90°#
Therefore to find #x# we can do this in several ways.
Say we didn't notice that we had a perpendicular angle or that the left side was equal to the right. If we only knew that the angles of line segment #bar(AB)# summed up to #180# we could have used the following equation: #47°+90°+x°=180# and solve for #x# which would have given us #43°#. Another way was knowing that we had perpendicular angles which is shown in the annotated image above.
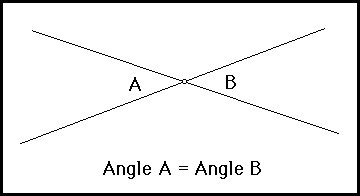
For #y#, you seemed to have realized the vertical angles which is to say...
Knowing that we are also dealing with supplementary angles whose angle sum is #180°#: (See example below)
Thus, to find #y# we can come up with an equation #47°+y°=180# and solve for #y# or simply #180°-47°# will give you the value of #y#. In either case, #y°=133#
#---------------------#
Question 2:
Again we have some vertical angles as well as a straight angle whose sum is #180°# that is divided into #3# angles. Knowing that if one vertical angle is #24°#, the other one is #24°# as well.
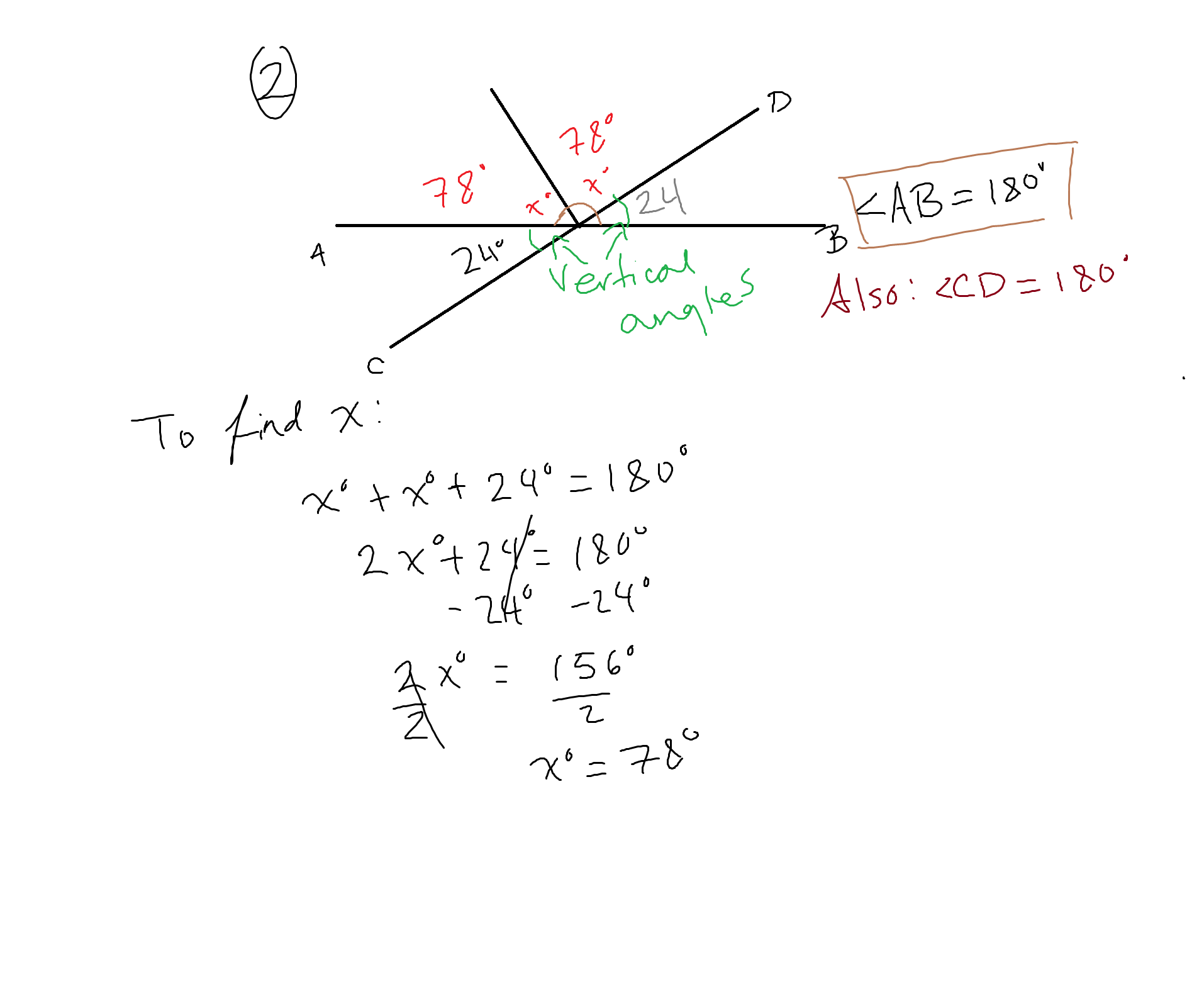
To find #x# we can therefore come up with the equation #2x+24=180# (#2x# because we have #2# #x#'s). We solve for #x# and find that the angles that make up the straight angle are #78°, 78°# and #24°#
#---------------------##
Question #3#:
Finally, we have this tricky one which requires you to do some algebra. We see some supplementary angles but we don't know what their angles are. Instead they are given to us in the form of an algebraic expression. Though we may not know what the angles are exactly, we do know that the sum of them will be #180°# Thus we have to find #x# by coming up with the following equation: #5x+45+3x-25=180#
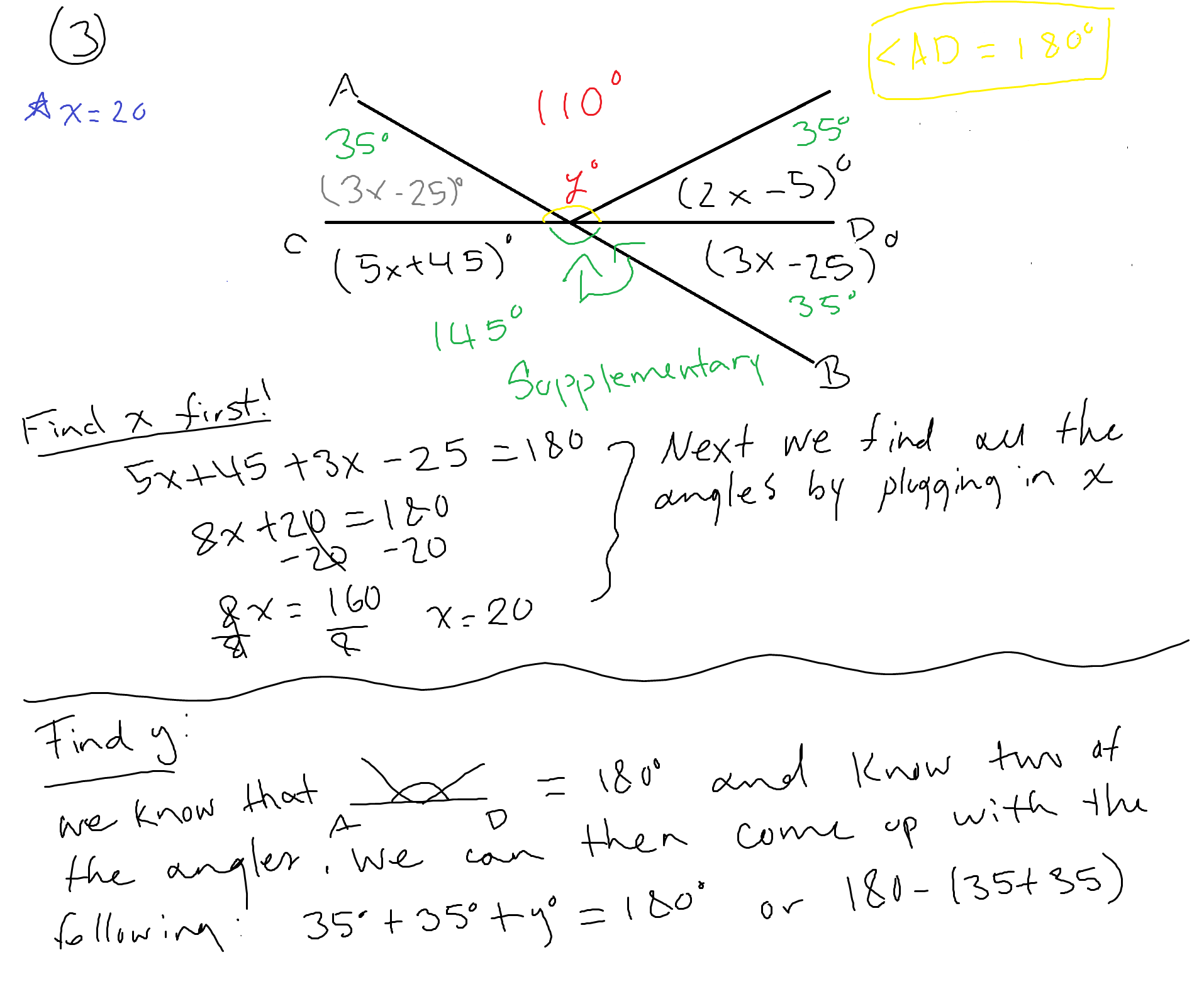
Once we find #x#, we substitute it to find all the angles except #y°#.
To find #y°# you must see that #/_CD# or that the angles that make up the line segment #bar(CD)# sum up to be #180°#. Therefore, #y°# can be found by setting up the equation: #35°+35+y°=180# or #180-(35+35)#. In either case, #y°=110°#
Whoo! That was a lot but I hope I helped! :)
![![enter image source here]](https://useruploads.socratic.org/q2TW89sDS4u7v9qJghDz_20170706_102632.jpg) (
( )
) ![![enter image source here]](https://useruploads.socratic.org/q2TW89sDS4u7v9qJghDz_20170706_102632.jpg) (
( )
) 






