Help me please, Two particles each of mass m, are joined by a thin string of length 2L, as shown in Figure 48. A uniform force F is applied in the middle of the string (x = 0) forming a right angle with the initial position of the string. Show that th????
Two particles each of mass m, are joined by a thin string of length 2L, as shown in Figure 48. A uniform force F is applied in the middle of the string (x = 0) forming a right angle with the initial position of the string. Show that the acceleration of each mass in the direction of 90 degrees with F is given #a_x=F/(2m)(x)/(L^2-x^2)^(1/2)#
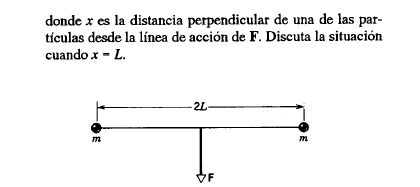
Two particles each of mass m, are joined by a thin string of length 2L, as shown in Figure 48. A uniform force F is applied in the middle of the string (x = 0) forming a right angle with the initial position of the string. Show that the acceleration of each mass in the direction of 90 degrees with F is given

1 Answer
See below
Explanation:
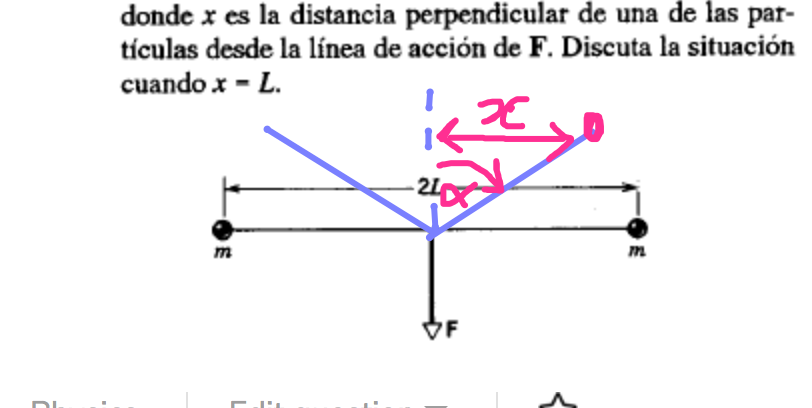
At all times, where co-ordinate
# F = 2 m ddot y implies ddot y = F/(2m)#
For each particle, resolving the tension
-
#T cos alpha = m ddot y# -
#T sin alpha = - m ddot x#
From the annotated drawing:
#tan alpha = x/(sqrt(L^2 - x^2))#
(NB: There is a minus sign as the
The Spanish bit then asks about
Well:
The solution appear to blow up.
But this equation doesn't mean anything at that point in time, as it is derived from there being some angle

