Help me solve this rational problem?

How do I solve this

How do I solve this
2 Answers
See explanation.
Explanation:
Given:
There are several things to note.
Thus we have
From this it MAY be the case that the question designer intended one of them to cancel out in the denominator.
As it is possible that there MAY be a cancelling out it is reasonable to explore
Note that
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
As the equation is undefined when the denominator becomes 0 we have a vertical asymptote at
Thus there is a horizontal asymptote at
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Although the
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
I will let you investigate this. You will need to shoe your logic in your solution.
We already know that there is a horizontal asymptote at
Test out what happens very close to the vertical asymptote.
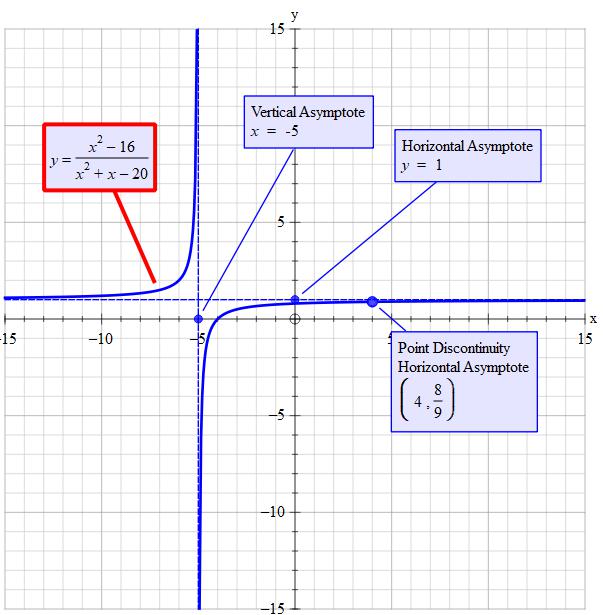
color(white)("d")
Explanation:
#"let "f(x)=(x^2-16)/(x^2+x-20)#
#"the numerator is a "color(blue)"difference of squares"#
#x^2-16=(x-4)(x+4)#
#"denominator"#
#"the factors of "-20" which sum to "+1#
#"are "+5" and "-4#
#x^2+x-20=(x+5)(x-4)#
#f(x)=(cancel((x-4))(x+4))/((x+5)cancel((x-4)))=(x+4)/(x+5)#
#" and denominator indicates a hole at"#
#x-4=0rArrx=4toy=(4+4)/(4+5)=8/9#
#"hole at "(4,8/9)#
#"the graph of "f(x)=(x+4)/(x+5)" is the same as"#
#(x^2-16)/(x^2+x-20)" but without the hole"# The denominator of f(x) cannot be zero as this would make f(x) undefined. Equating the denominator to zero and solving gives the value that x cannot be and if the numerator is non-zero for this value then it is a vertical asymptote.
#"solve "x+5=0rArrx=-5" is the asymptote"#
#"Horizontal asymptotes occur as"#
#lim_(xto+-oo),f(x)toc" ( a constant)"#
#"divide terms on numerator/denominator by "x#
#f(x)=(x/x+4/x)/(x/x+5/x)=(1+4/x)/(1+5/x)#
#"as "xto+-oo,f(x)to(1+0)/(1+0)#
#y=1" is the asymptote"#
#"there is a discontinuity at "x=-5#
#"domain is "x in(-oo,-5)uu(-5,oo)#
#"there is a discontinuity at "y=1#
#"range is "y in(-oo,1)uu(1,oo)#
#"For Intercepts"#
#x=0rArry=4/5larrcolor(red)"y-intercept"#
#x+4=0rArrx=-4larrcolor(red)"x-intercept"#
graph{(x+4)/(x+5) [-10, 10, -5, 5]}

