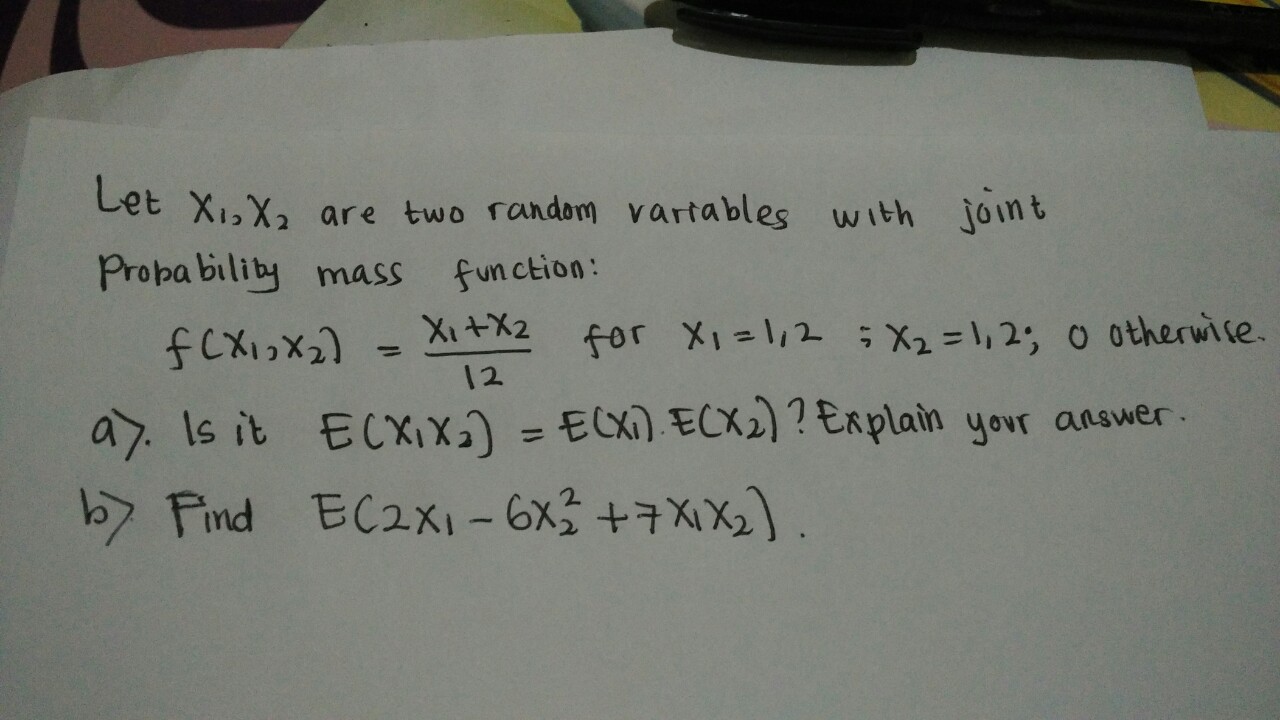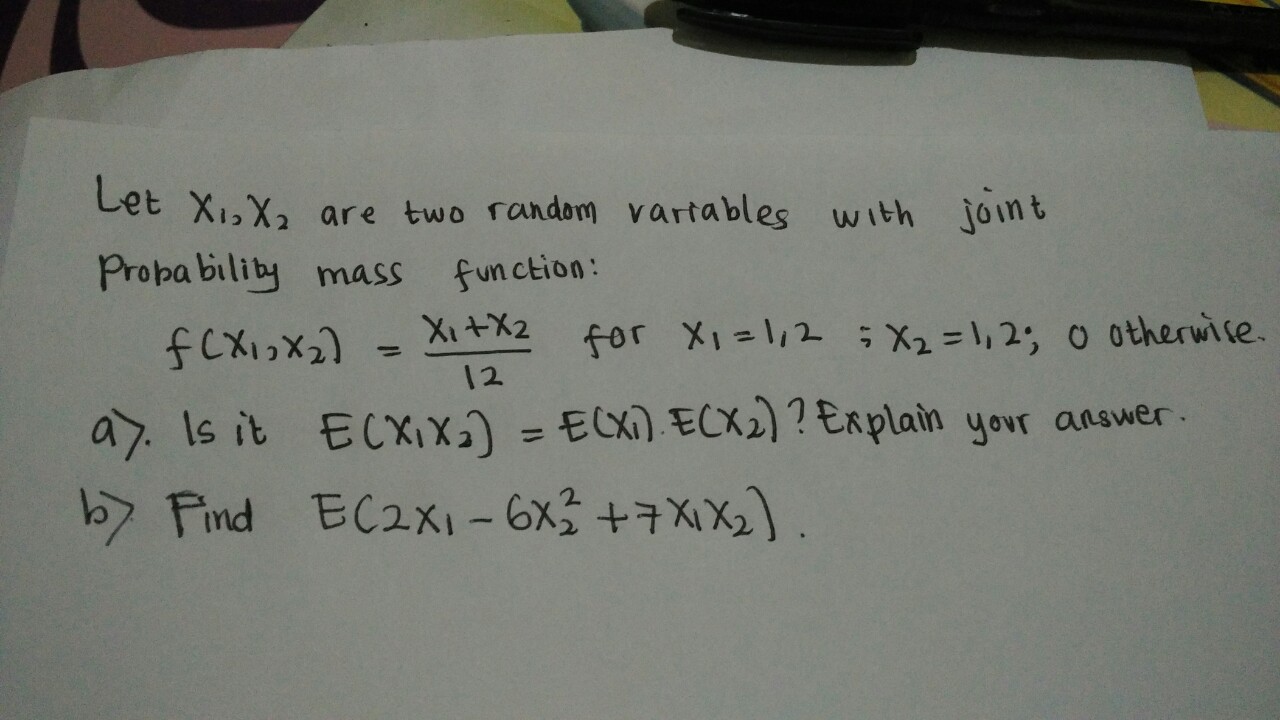Help me to solve this problem please? I really need help to solve about joint probability mass function..

enter image source here

1 Answer
MattyMatty
Apr 9, 2018

#"a) No"#
#"b) 25/6"#

Explanation:

#"So we have"#
#f(1,1) = 1/6#
#f(1,2) = 1/4#
#f(2,1) = 1/4#
#f(2,2) = 1/3#
#E(X_1 X_2) = (1/6)*1+(1/4)*2+(1/4)*2+(1/3)*4 = 2.5#
#E(X_1) = (1/6 + 1/4)*1 + (1/4 + 1/3)*2 = 19/12#
#E(X_2) = (1/6 + 1/4)*1 + (1/4 + 1/3)*2 = 19/12#
#"So "E(X_1 X_2) != E(X_1) E(X_2)#

#E(2 X_1 - 6 X_2^2 + 7 X_1 X_2)#
#= 2 E(X_1) - 6 E(X_2^2) + 7 E(X_1 X_2)#
#= 19/6 - 6 E(X_2^2) + 7 * 2.5#

#E(X_2^2) = (1/6 + 1/4)*1 + (1/4 + 1/3)*4 = 33/12#

#= 19/6 - 6 * 33/12 + 7 * 2.5#
#= 19/6 - 33/2 + 17.5#
#= 19/6 + 1#
#= (19+6)/6#
#= 25/6#

Related questions
Impact of this question
994 views around the world
You can reuse this answer
Creative Commons License