Define auto redox reaction. Balance the following equation by ion-electron or oxidation number method: #"K"_2"Cr"_2"O"_7(aq) + "FeSO"_4(aq) + "H"_2"SO"_4(aq) -> "K"_2"SO"_4(aq) + "Cr"_2("SO"_4)_3(s) + "Fe"_2("SO"_4)_3(s) + "H"_2"O"(l)#?
2 Answers
An Auto-redox reaction [1] is a redox reaction in which a substance act as both the oxidizing agent and the reducing agent.
Balanced chemical equation:
Explanation:
Start by identifying reducing and oxidizing agents.
Chromium atoms are reduced; the oxidation state of this element decrease from
Reduction half:
Add water to the product side and protons (i.e.,
Iron (II) sulfate is oxidized to iron (III) sulfate; therefore iron (II) sulfate undergoes oxidation and acts as the reduction agent.
Oxidation half:
Electrons should cancel out in the net reaction; each mole of the reduction half reaction consumes six moles of electrons while each mole of the oxidation half produces one moles; electrons will cancel out in the sum if coefficients of the reduction half reaction are expanded by a factor of six:
Combining reactions of the reduction half and six times that of the oxidation half gives:
That is:
Pair ions with spectator ions of the respective opposite charges as seen in the unbalanced reaction given:
Anion reactants pair with potassium ions
Cation reactants pair with sulfate ions
Hence the net chemical equation would be
References
[1] "AUTO OXIDATION REDUCTION REACTION," City Collegiate, http://www.citycollegiate.com/auto_oxidation.htm
Jacob T. has answered the second half of the question; however, I think that the example provided from the question isn't really an auto-redox reaction since different species oxidize and reduce in the given reaction.
Instead, I'll give an example of a disproportionation reaction, which would follow the definition of an "auto-redox" reaction, where the same species gets oxidized and reduced.
The result is:
#2stackrel(color(blue)(+3))("Mn")_2"O"_3(s) + 4"H"^(+)(aq) -> 2stackrel(color(blue)(+4))("Mn")"O"_2(s) + 2stackrel(color(blue)(+2))("Mn"^(2+))(aq) + 2"H"_2"O"(l)#
Consider the diagram below:
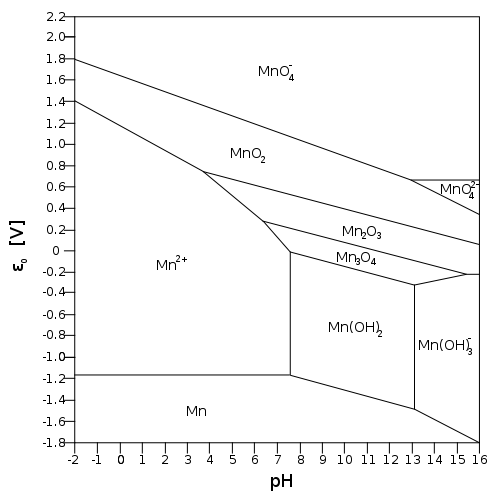
Manganese(III) oxide can get oxidized to
#"Mn"_2"O"_3(s) -> "MnO"_2(s)#
First, balance the non-oxygen atoms.
#"Mn"_2"O"_3(s) -> color(blue)(2)"MnO"_2(s)#
Then balance the oxygen atoms with water.
#color(blue)("H"_2"O"(l)) + "Mn"_2"O"_3(s) -> 2"MnO"_2(s)#
Balance the hydrogen atoms with
#"H"_2"O"(l) + "Mn"_2"O"_3(s) -> 2"MnO"_2(s) + color(blue)(2"H"^(+)(aq))#
Balance the charge with
#color(green)("H"_2"O"(l) + "Mn"_2"O"_3(s) -> 2"MnO"_2(s) + 2"H"^(+)(aq) + 2e^(-))#
Now, the other half-reaction is for the reduction, also of
Let's say we are below pH 6. Then:
#"Mn"_2"O"_3(s) -> "Mn"^(2+)(aq)#
Repeat the same steps as before to get the reduction half-reaction:
#color(green)(2e^(-) + 6"H"^(+)(aq) + "Mn"_2"O"_3(s) -> 2"Mn"^(2+)(aq) + 3"H"_2"O"(l))#
Now, add these together to cancel out the electrons.
#"H"_2"O"(l) + "Mn"_2"O"_3(s) -> 2"MnO"_2(s) + 2"H"^(+)(aq) + cancel(2e^(-))#
#ul(cancel(2e^(-)) + 6"H"^(+)(aq) + "Mn"_2"O"_3(s) -> 2"Mn"^(2+)(aq) + 3"H"_2"O"(l))#
#cancel("H"_2"O"(l)) + "Mn"_2"O"_3(s) + cancel(6)^(4)"H"^(+)(aq) + "Mn"_2"O"_3(s)#
#-> 2"MnO"_2(s) + cancel(2"H"^(+)(aq)) + 2"Mn"^(2+)(aq) + cancel(3)^(2)"H"_2"O"(l)#
Cancel out the
#bb(2stackrel(color(blue)(+3))("Mn")_2"O"_3(s) + 4"H"^(+)(aq) -> 2stackrel(color(blue)(+4))("Mn")"O"_2(s) + 2stackrel(color(blue)(+2))("Mn"^(2+))(aq) + 2"H"_2"O"(l))#


