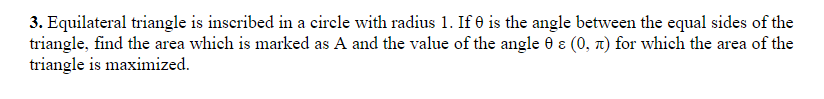Solution supposed the problem is about isosceles triangle.
#r=1# so #(OB)=(OC)=1#
From the right triangle #OhatBM#:
- #sinθ=(BM)/(OB)# #<=># #(BM)=(OB)*sinθ=1*sinθ#
and #(BC)=2(BM)=2sinθ# ,
- #cosθ=(OM)/(OB)# #<=># #(OM)=cosθ*(OB)=1*cosθ#
Thus,
#(AM)=(OA)+(OM)=1+cosθ#
so Area will be
#A_(rea)=A(θ)=1/2*(BC)*(AM)=1/2*2sinθ(1+cosθ)# #=#
#sinθ(1+cosθ)#
#Α'(θ)=(sinθ(1+cosθ))'# #=#
#(sinθ)'(1+cosθ)+sinθ(1+cosθ)'# #=#
#cosθ(1+cosθ)+sinθ*(-sinθ)# #=#
#cosθ+cos^2θ-sin^2θ# #=#
#cos2θ+cosθ#
(used the trigonometric identity #cos^2x-sin^2x=cos2x#
/ proof can be found here https://socratic.org/questions/how-do-you-prove-cos2x-cos-2x-sin-2-using-other-trigonometric-identities)
#A'(θ)=0# #<=>#
#cos2θ+cosθ=0# #<=>#
#cos2θ=-cosθ# #<=>#
#cos2θ=cos(π-θ)# #<=>#
graph{cosx [-0.883, 3.984, -1.187, 1.246]}
#2θ=π-θ#
#θ##in##(0,π)#
so #θ=π/3#
- For #0<# #θ<π/3# for example #θ=π/6# we see that #A'(θ)>0#
as a result #A# is strictly increasing in #[0,π/3]#
- For #π/3<θ<π# for example #θ=π/2# we see that #A'(θ)<0#
as a result #A# is strictly decreasing in #[π/3,π]#
because #A'(π/6)=cos((2π)/6)+cos(π/6)=cos(π/3)+cos(π/6)#
#=1/2+sqrt3/2>0#
#A'(π/2)= cos((2π)/2)+cos(π/2)=cosπ+cos(π/2)=-1<0#
#A# is increasing at #[0,π/3]# and decreasing at #[π/3,π]#
and has a local maximum at #θ_0=π/3# with #A(π/3)=sin(π/3)(1+cos(π/3))=sqrt3/2(1+1/2)=(3sqrt3)/4#
- Therefore, we have #A_(rea)# maximum value when #θ=π/3# and the value is #(3sqrt3)/4#
NOTE: Alternative solution to #A'(θ)=0# which is pretty straightforward and doesn't require further trigonometric examination would be the following
#cosθ+cos^2θ-sin^2θ=0# #<=># #cosθ+cos^2θ-(1-cos^2θ)=0# #<=># #(2cosθ-1)(cosθ+1)=0# and since #θ##in##(0,π)# we get
#cosθ=1/2# so #θ=π/3#