How about solution. ( I = ?)
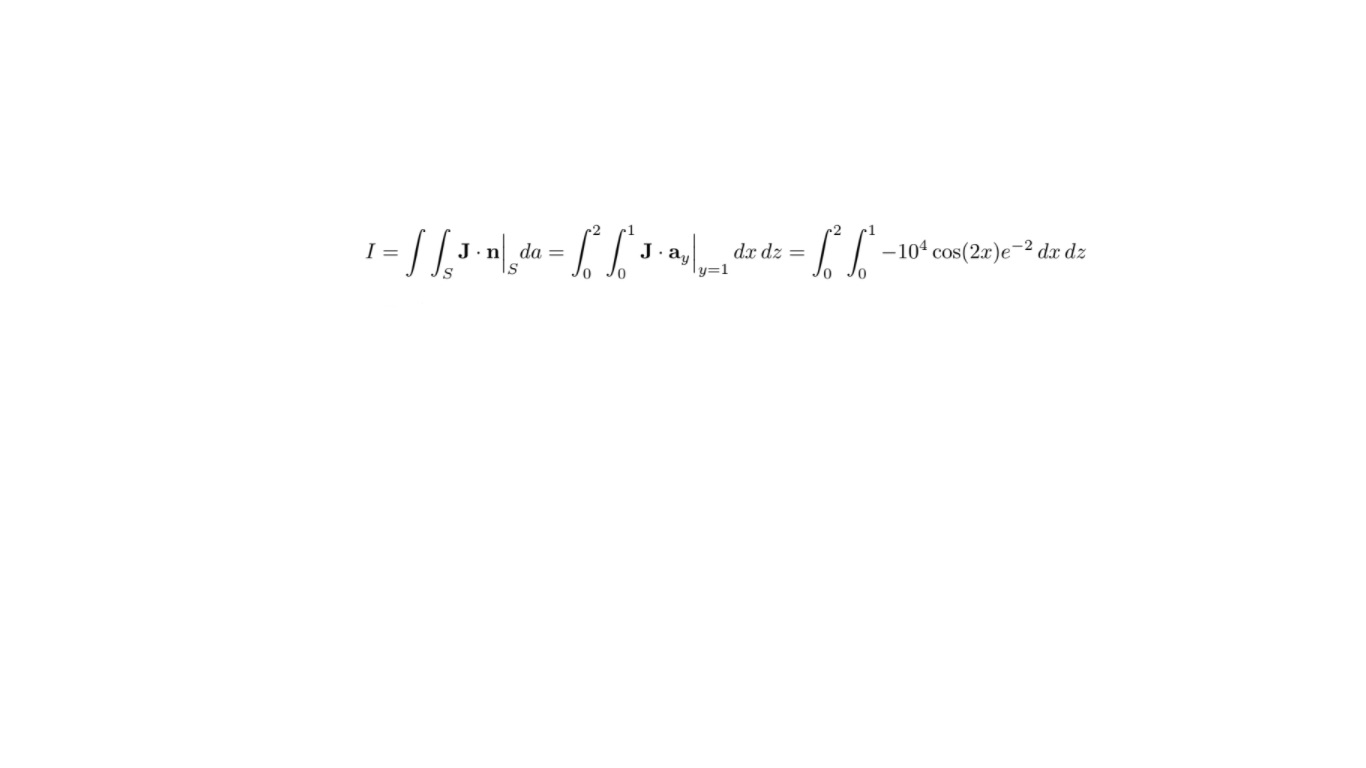
2 Answers
Explanation:
We wish to know what the following integral evaluates to:
Start by removing the constants from the integrand.
We will let
Integrate
Integrate the (constant) term
Finally, substitute our original constants back into
This is our final answer.
Given
#I = int_0^2 int_0^1 -10^4 cos(2x) e^(-2) dx dz#
#=>I = -10^4 e^(-2) int_0^2 int_0^1 cos(2x) dx dz#
First Integrate outer integral with respect to
#I = -10^4 e^(-2) | (int_0^1 cos(2x) dx)z|_0^2 #
#=>I = -10^4 e^(-2)xx2 int_0^1 cos(2x) dx #
Now Integrate with respect to
#I = -10^4 e^(-2)xx2 | 1/2 sin(2x) |_0^1 #
#=>I = -10^4 e^(-2) sin2#

