Question

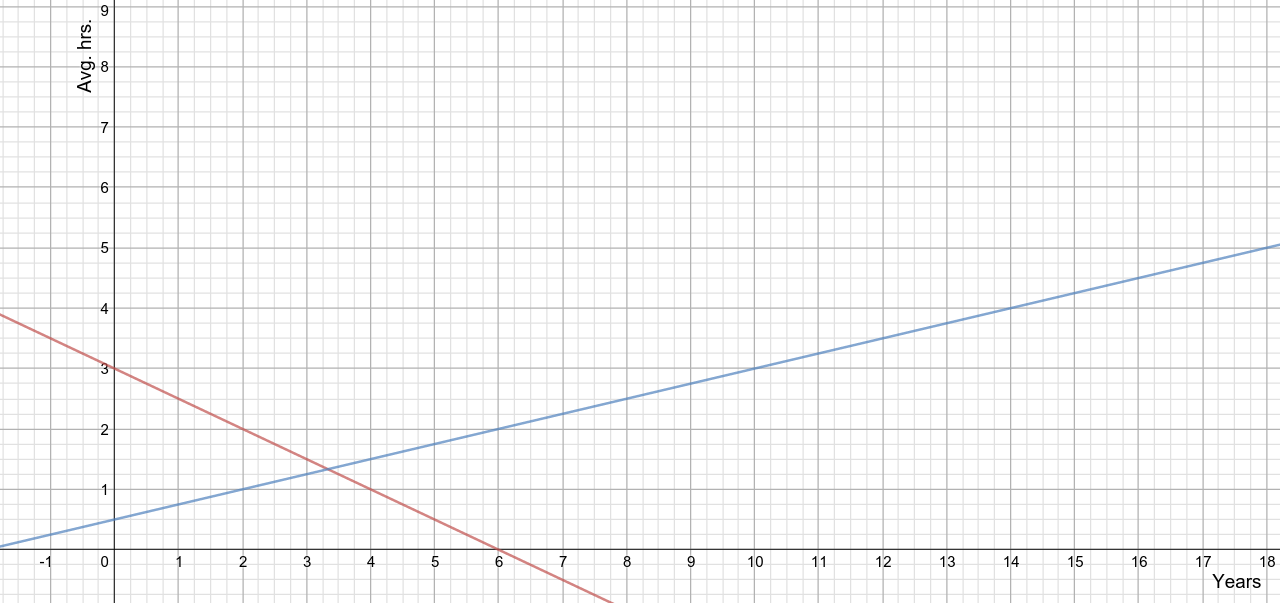
How can a system of equations be used to predict media use?

Answer 1

Suppose we have collected data about media use, as follows:

Prnt media:
- year 0 (1994) `->` 3 hrs per person per day
- year 1 (1995) `->` 2.5 hrs per person per day
- ...

Online media:
- year 0 (1994) `->` 0.5 hrs per person per day
- year 1 (1995) `->` 0.75 hrs per person per day - ...
- ...

We assume a simple, linear model, so that we can easily fill in the yearly data and we already have sufficient information to determine the equations.

Let's denote by `x` the number of years passed since 1994 and by `y` the average number of hours per person per day spent on media use .

Our linear equations will have the general form `y=ax+b`

For print media use we have:
`ax+b = 3` when `x = 0` `->` `b = 3`
and `ax+b = 2.5` when `x=1` `->` `a+b=2.5` `->` `a=-0.5`
Therefore, our equation for print media use is `y = -0.5x+3`

For online media use we have:
`ax+b=0.5` when `x=0` `->` `b=0.5`
and `ax+b=0.75` when `x=1` `->` `a+b=0.75` `->` `a=0.25`
Therefore, our equation for online media use is `y=0.25x+0.5`

Now, we have a system of two linear equations allowing predictions of media use at various data points. (Of course, this is a fictitious example and an oversimplification meant just to illustrate the general idea. We can build a more realistic model by using exponential instead of linear functions).