Question

How can I calculate maximum velocity in simple harmonic motion?

I know that the equation for velocity is

`V= -omega Asin(omega t +phi`)

supposing `phi` to be zero , cuz if the object is released from the mean position then, at the mean position displacement is zero so,

`sin phi` = 0 →`phi` = 0.

I know from the velocity time graph for SHM that max velocity = `Aomega`.

That is the argument must be -1

How will that be possible ? the argument can only be zero for `2pi/3` right?

Am I missing something?

Answer 1

`"Please see the following explanations."`

Explanation:

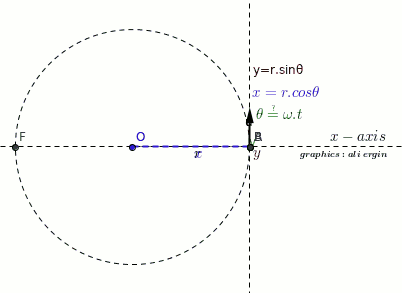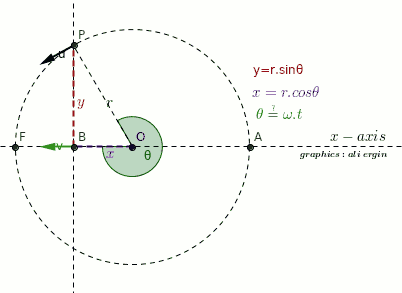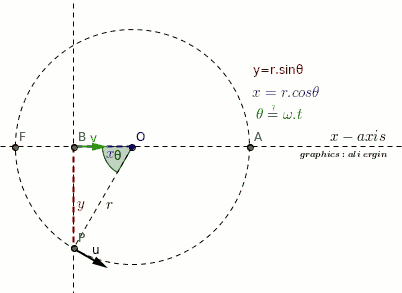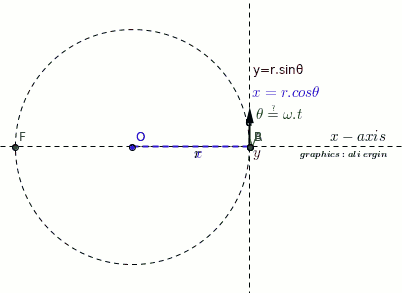
• we recommend that you first watch the animation carefully

• Let P be a point rotating around the O point at a constant linear velocity(u).

• The projection of P on the x-axis is point B.

• The movement of point B is limited between A and F.

• The simple harmonic motion is the action of point B.

• Please note that the velocity vector changes direction.

• At points A and F, the velocity of B is zero(green vector).

• The greatest velocity B has is at O.`theta=pi/2 and theta=(3pi)/2`

`x=r cos theta`

`theta=omega.t`

`x=r. cos(omega t)`

`(d x)/(d t)=v`

`(d x)/(d t)=v=-r omega sin omega t`

`"if "omega t=pi/2" or "omega t=(3pi)/2" , "v=-r omega("maximum velocity")`

`v_("max")=- r omega`

`"or :"`

`y=r sin theta`

`(d x)/(d t)=v=- omega y`

`x^2+y^2=r^2`

`y=sqrt(r^2-x^2)`

`v=- omega sqrt(r^2-x^2)`

`"if "x=0 " "v=v_("max")`