How can I calculate the titration of a weak acid and a strong base?
1 Answer
There are some critical pH values you will need to calculate
- At the very beginning
- At the equivalence point
- Between neutralization and the equivalence point
- After the equivalence point
Assume that you are titrating 25 mL of 0.1 mol/L
At the beginning
You know from your ICE table that
At the equivalence point
You know that the equivalence point will be at 25 mL of
The
At points between 0 mL and the equivalence point
Use the Henderson-Hasselbalch Equation.
Calculate the moles of
For example, at 12.5 mL, you will have added 0.001 25 mol of base. You will have neutralized 0.001 25 mol of
After the equivalence point
You will just be adding excess moles of
Calculate the excess moles, divide by the volume to get the molarity. Then calculate the pOH and the pH.
For example, after 40 mL of base, you will have added 0.004 mol of
You will have 0.0015 mol of
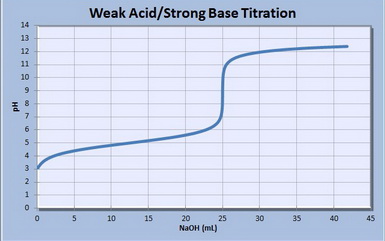
Your calculated values should match the graph below.