1) to find length #BE#
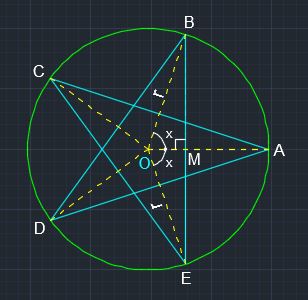
Let #O# be the center of the circle.
Let #angleAOB=x#
#=> anglex=360/5=72^@#
Consider #DeltaOBE#,
As #OB=OE=r=25# cm
#=> DeltaOBE# is isosceles
#=> angleOBE=angleOEB#,
#=> M# is the mid-point of #BE#
#=> DeltaOMB and DeltaOME# are two congruent right triangles.
#=> BM=rsinx#
#=> BE=2*BM=2rsinx#
#=2*25*sin72=2*25*(sqrt(10+2sqrt5)/4)#
#=(25sqrt(10+2sqrt5))/2~~47.55# cm
2) to find length #BA# or length #BF#
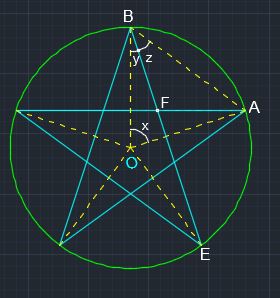
#DeltaBOE# is isosceles
#x=360/5=72^@#
#=> y=(180-2x)/2=(180-144)/2=18^@#
#BOA# is also isosceles.
#=> angleOBA=(180-x)/2=(180-72)/2=54^@#
#=> angleFBA=z=54-18=36^@#
#=> BA=2rsin(x/2)=2*25*sin36#
#=2*25*(sqrt(10-2sqrt5))/4=(25sqrt(10-2sqrt5))/2~~29.39# cm
#DeltaBFA# is also isosceles.
#=> 2*BF*cosz=BA#
#=> BF=(BA)/(2*cosz)=(BA)/(2*cos36)#
#=1/2*(25sqrt(10-2sqrt5))/2*4/(sqrt5+1)#
#=(25sqrt(10-2sqrt5))/(sqrt5+1)~~18.16# cm
