How can I graph an RC circuit?
1 Answer
If you don't remember the concept, then if you can derive the formula, it will be very easy to graph.
With a basic RC circuit, you have:
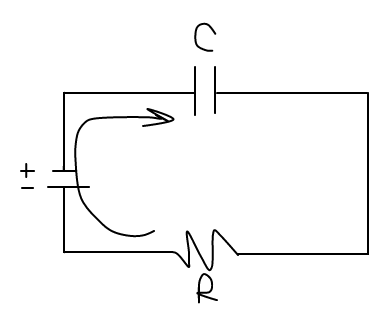
So, going clockwise, you get a change in voltage for a closed circuit to follow Kirchoff's law.
#DeltaV = 0 = epsilon - V_C - V_R# where
#epsilon# is the "electromotive force" (the voltage increase through the battery),#V_C# is the voltage drop through the capacitor as it stores charge on the parallel plates, and#V_R# is the voltage drop through the resistor.
I recall that the capacitance
Furthermore, the current can be written as the change in charge over time, since the capacitor is going to store charge over time
#epsilon = q/C + IR#
Multiply by
#epsilonC = q + (dq)/(dt)RC#
#-(dq)/(dt)RC= q - epsilonC#
Separate the variables such that
#int_(0)^(q) 1/(q - epsilonC)dq = int_(0)^(t) -1/(RC)dt#
#ln|q - epsilonC| - ln|-epsilonC| = -t/(RC)#
Using the properties of logarithms, you can turn the left side into a fraction:
#ln|(q - epsilonC)/(-epsilonC)| = -t/(RC)#
and then exponentiate both sides. Also note that
#(q - epsilonC)/(-epsilonC) = e^"-t/RC"#
#q - epsilonC = -epsilonCe^"-t/RC"#
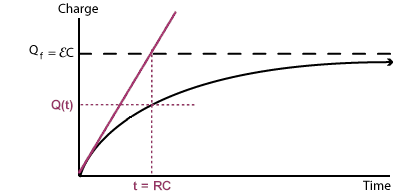
#color(blue)(q(t) = epsilonC(1 - e^"-t/RC"))#
So you can graph the charge with respect to time as it gets stored into the capacitor using this equation. All you have to do is note that it is the vertical reflection of an exponential decay, seen as
Then, at
Or, if you want to graph the current
#color(blue)(I = (dq)/(dt)) = d/(dt)[epsilonC - epsilonCe^"-t/RC"]#
#= -epsiloncancel(C)*-1/(Rcancel(C))e^"-t/RC"#
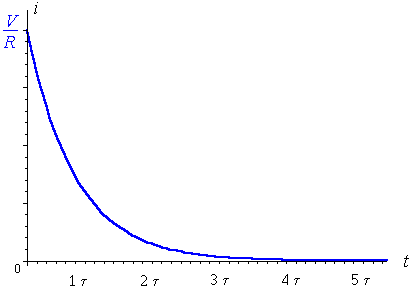
#= color(blue)(epsilon/R e^"-t/RC")#
This one you can indeed see is exponential decay from the
where

