How can I solve the equation for this interval, (see picture)? Thanks!
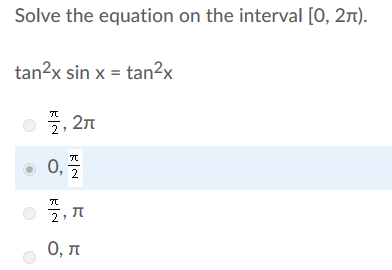
2 Answers
Explanation:
Rewrite the equation as
So, either
In the interval
On the other hand,
Thus, the possible values of
Note : None of the options given in the picture are correct (or, if you are not looking for all solutions, the lower three are)!
While
The solutions are
Explanation:
Treat the problem like a quadratic; factor it, then set the factors equal to
Now set each of the factors equal to zero:
Since
The other two work, so they are real solutions to the problem.


