How can I tell if this is convergent or divergent?
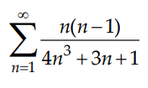
I'm not sure what test to use. Any help is really appreciated.
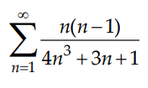
I'm not sure what test to use. Any help is really appreciated.
1 Answer
It is divergent, by comparison with the harmonic series.
Explanation:
Given:
#sum_(n=1)^oo (n(n-1))/(4n^3+3n+1)#
Quick assessment
For large values of
Comparison test
We can make a comparison test with a multiple of the harmonic series by noting that:
-
The first term of the sum is
#0# . Though this does not matter for us in terms of convergence or divergence, it does mean we can ignore it in our expressions below. -
#(n-1) >= n/2# for all#n >= 2# -
#4n^3+3n+1 < 5n^3# for all#n >= 2#
So:
#sum_(n=1)^oo (n(n-1))/(4n^3+3n+1) >= sum_(n=2)^oo (n^2)/(10n^3) >= 1/10 sum_2^oo 1/n = +oo#

