How can we convert #DeltaH_f^@# at 298K to #DeltaH_f^@# at different temperatures ?? Also tell how to convert bond energy at 298K to bond energy at different temperature
1 Answer
You'd need to heat the product from standard temperature to nonstandard temperature at the same pressure and add that heating enthalpy.
However, I don't think bond enthalpy changes significantly at a different temperature. We can think of it like an activation energy for that particular molecule's dissociation reaction (in the gas phase to keep it simple):
#"AB"(g) -> "A"(g) + "B"(g)#
Activation energy is almost completely temperature independent, so we can assume that so is bond enthalpy.
Suppose you have the
#3"H"_2(g) + "N"_2(g) -> 2"NH"_3(g)# ,
and suppose the reactant concentrations were constantly replenished such that the equilibrium is constantly pushed way towards
The
This is the thermodynamic cycle for this process, to get the big picture:
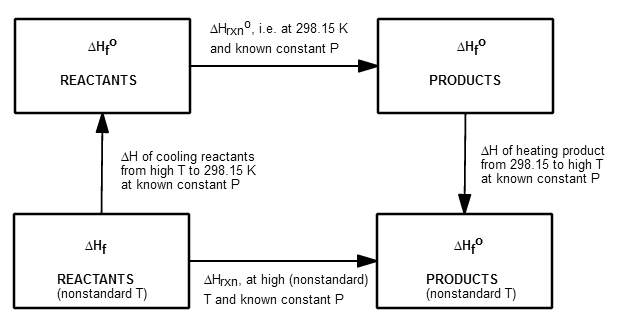
Usually we know
#DeltaH_(T_1)^(T_2) = int_(T_1)^(T_2) C_P dT#
This requires that you know the constant-pressure heat capacity of
your compound(s) and that you assume that it stays constant in the relevant temperature range.
http://webbook.nist.gov/cgi/cbook.cgi?ID=C7664417&Type=JANAFG&Plot=on
a
So, from using the average
#DeltaH_(298.15)^(500) = int_(298.15)^(500) (42.01 + 35.64)/2 dT#
#~~ 38.825T_2 - 38.825T_1#
#= 38.825DeltaT#
#=# #38.825(500 - 298.15)#
#=# #"7836.83 J/mol"# #-># #"7.937 kJ/mol"# (notice the resemblance to "
#q = mc_sDeltaT# ".)
The
#(-45.94 + 7.937)# #"kJ/mol"# #~~ color(blue)(-"38.10 kJ/mol")#
It's less negative at a higher temperature, meaning that it is less exothermic to form
This makes physical sense because we are just assuming the heat released due to making it at a lower temperature is re-absorbed to heat the surroundings further (thus making the enthalpy released less negative).

