[1] Junction Rule: Junction rule is a consequence of charge conservation, subjected to the assumption that there is no accumulation or depletion of charge anywhere in the circuit.
Stated formally, the algebraic sum of all the currents at a junction is zero.
#\sum_k i_k = 0#
No Accumulation/Depletion Assumption: #(\delQ)/(\delt)=0# ...... (Eq 1)
Equation of Continuity : Mathematical statement of Charge Conservation condition.
#\grad.vecJ + \frac{\del\rho}{\delt} = 0# ...... (Eq 2)
#vec J# is the current density and #\rho# is the charge density.
This is applicable everywhere inside the volume of the circuit. So we can take the volume integral on both sides,
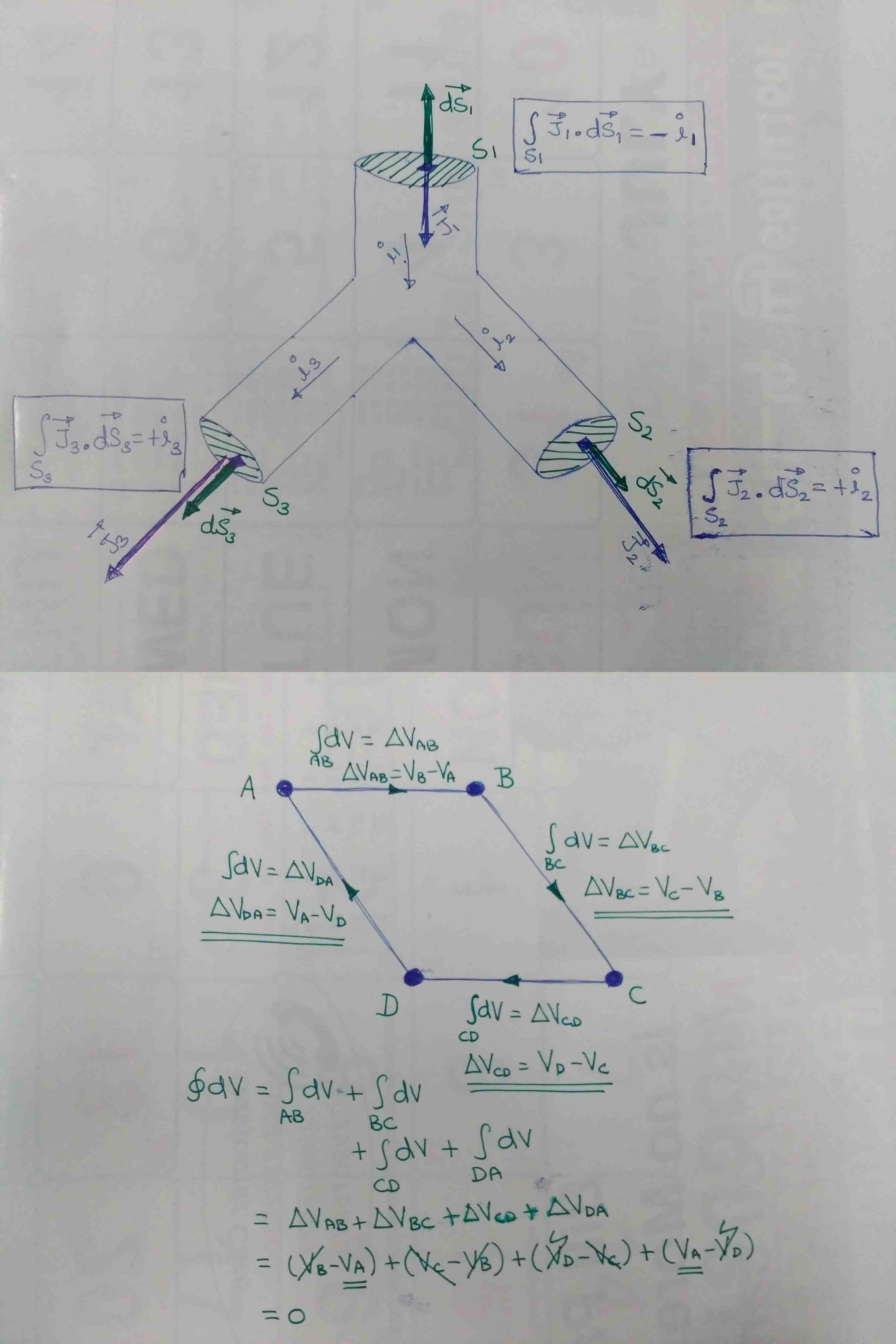
Let us consider a volume centred around a junction as shown in the top figure (attached).
#\int_{V}[\grad.vecJ + \frac{\del\rho}{\delt}]dV = 0#
#\int_{V}\grad.vecJ dV = -\frac{\del}{\delt}\int_{V}\rhodV=-(\delQ)/(\delt).#
Volume integral of the charge density #\rho# is the total charge #Q# inside the volume, which is a constant because of the assumption that we made, (No charge accumulation/depletion in the volume, Eq 1)
#\int_{V}\grad.vecJ dV =-cancel{(\delQ)/(\delt)} = 0.# ...... (Eq 3)
By Gauss Divergence Theorem we can convert the volume integral of the left-hand-side of Eq 3 into a closed surface integral over the surface bounding this volume,
Gauss's Divergence Theorem: #\oint_{S}\quad vecJ.dvecS = \int_{V}grad.vecJdV#
Therefore Eq 3 becomes,
#\oint_{S}vecJ.dvecS = 0# ...... (Eq 4)
The surface integral can be done in parts. The entire surface enclosing the volume can be partitioned into three cross-sectional surfaces #S_1, S_2# and #S_3# and a peripheral surface (please refer to figure). But the integrand vanishes everywhere on the peripheral surface, because the surface normal on the peripheral surface is perpendicular to the current density vector.
Therefore,
#\oint_{S}vecJ.dvecS = \int_{S_1}vecJ_1.dvecS_1 + \int_{S_2}vecJ_2.dvecS_2 + \int_{S_3}vecJ_3.dvecS_3 =0 #
Surface integral of current density is the total current through the cross-section :
#\int_S\quadvecJ.dvecS = i#
Current #i_1# enters the volume through the cross-sectional surface #S_1# and branches out into #i_2# and #i_3#. Current #i_2# exits the volume through the cross-sectional surface #S_2# and current #i_3# exits the volume through the cross-section surface #S_3#.
On surface #S_1#, the surface normal is anti-parallel to the current density vector. So it must yield a negative value.
#\int_{S_1}vecJ_1.dvecS_1 = -i_1#
On surface #S_2#, the surface normal is parallel to the current density vector. So it must yield a positive value.
#\int_{S_2}vecJ_2.dvecS_2 = +i_2#
On surface #S_3#, the surface normal is parallel to the current density vector. So it must yield a positive value.
#\int_{S_3}vecJ_3.dvecS_3 = +i_3#
#\oint\quadvecJ.dvecS = -i_1 + i_2 + i_3 = 0#
In general, #\quad \sum_k i_k = 0# (Junction Rule)
[2] Loop Rule: Loop rule is a consequence of the fact that when the electric field is a conservative force field, then the work done in moving a test charge around a closed loop is zero.
The condition for the electric field to be a conservative force field is that there should not be any time varying magnetic flux linked to the circuit.
ie. #\quad \frac{\del\Phi_B}{\delt} = 0#
Stated formally, the algebraic sum of the voltage differences across all the circuit elements along a closed loop is zero.
#\sum_k \DeltaV_k = 0#
The work done in moving a test charge #q_0# around a closed path in a conservative electric force field is zero.
#W = \oint \quad vecF.dvecr = q_0 \oint \quad vecE.dvecr = 0;#...... (Eq 5)
If the electric field is conservative field, it can be expressed as the gradient of a scalar potential function.
#vec E = -\gradV; \qquad "Remember" \quad gradV.dvecr = dV#
Therefore Eq 5 becomes,
#\oint \quad vecE.dvecr = \oint \quad gradV.dvecr = \oint \quad dV = 0#
Now consider a closed path #A\rightarrowB\rightarrowC\rightarrowD\rightarrowA# as shown in the bottom figure (attached).
#\oint\quad dV = \int_{AB}\quad dV + \int_{BC}\quaddV + \int_{CD}\quaddV + \int_{DA}\quaddV = 0#
#\DeltaV_{AB} + \DeltaV_{BC} + \DeltaV_{CD} + \DeltaV_{DA} = 0;#
In general, #\quad \sum_k \DeltaV_k = 0# (Loop Rule)