How can you identify critical points by looking at a graph?
1 Answer
Please read the explanation.
Explanation:
Definition of a Critical Point:
A continuous function
-
#color(blue)(f'(x)=0# -
#color(blue)(f'(x)# is undefined.
A critical point can be a local maximum if the functions changes from increasing to decreasing at that point OR
a local minimum if the function changes from decreasing to increasing at that point.
Let us consider the Sin Graph:
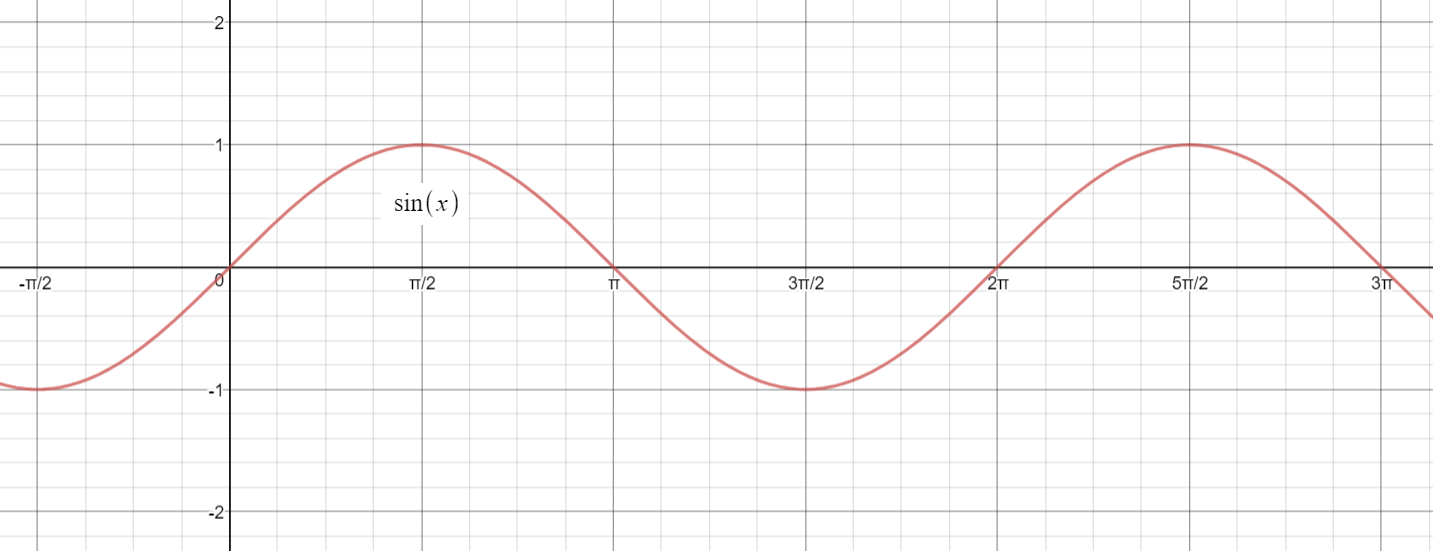
One Period of this graph is from
The graph does not go above
View the graph below:
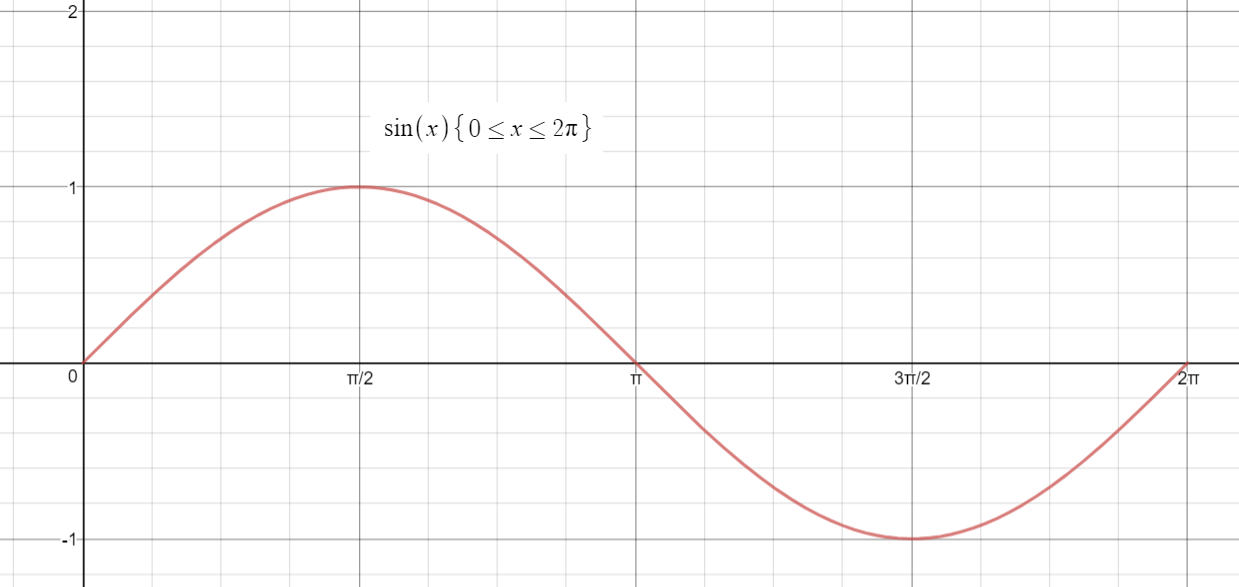
Note that the graph starts from
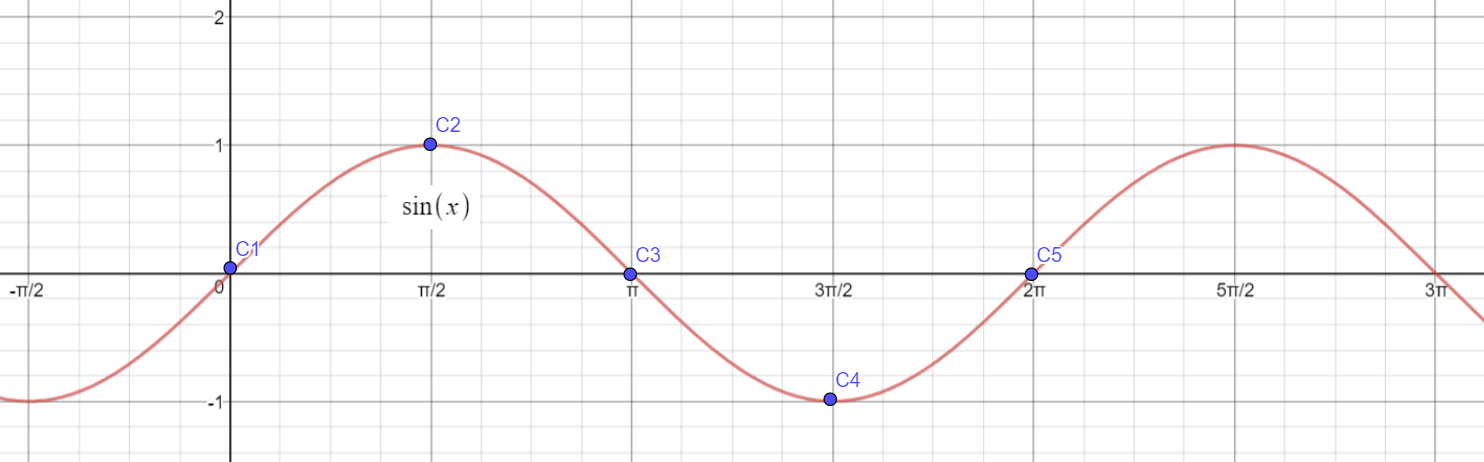
Observe that the points
We have a maximum at the point
Critical Points:
Formula :
Note that the distance between the points:
are all equal and there are four of them.
Hence,
and the Critical Points are
and the distance between any two critical point is
Hope this helps.

