How do colligative properties affect freezing point?
1 Answer
Colligative properties cause freezing point depression.
Explanation:
If you examine the following graph:
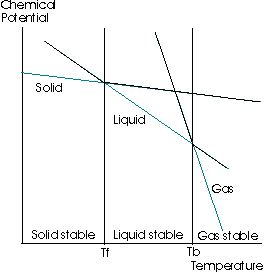
It shows the change in the chemical potential of a solution versus a change in the temperature, at a constant pressure. (All compounds want to minimize chemical potential, similar to minimizing energy.)
There is an equation which describes colligative properties:
#\mathbf(mu_j = mu_j^"*" + RTlna_j)# where
#mu_j# is the chemical potential of a solvent#j# that already contains some amount of solute,#mu_j^"*"# means pure solution (i.e. just the solvent without added solute), and#a_j# means activity of solvent#j# in the solution.
The activity is defined as:
#a_j = x_jgamma_j# where
#x_j# is mole fraction of compound#j# and#gamma_j# is the activity coefficient of compound#j# . Thus, you can infer that a lower mole fraction of compound#j# gives a lower activity and vice versa.
Since mole fractions are always
Because of this, and because of the fact that
What this says, then, is that the chemical potential decreases, and so on the graph above, if you are examining a liquid's freezing point, move the straight line that corresponds to the liquid downwards a certain amount.
You would see that the freezing point is shifted left, and the boiling point is shifted right.
Therefore, colligative properties cause freezing point depression (and boiling point elevation).


