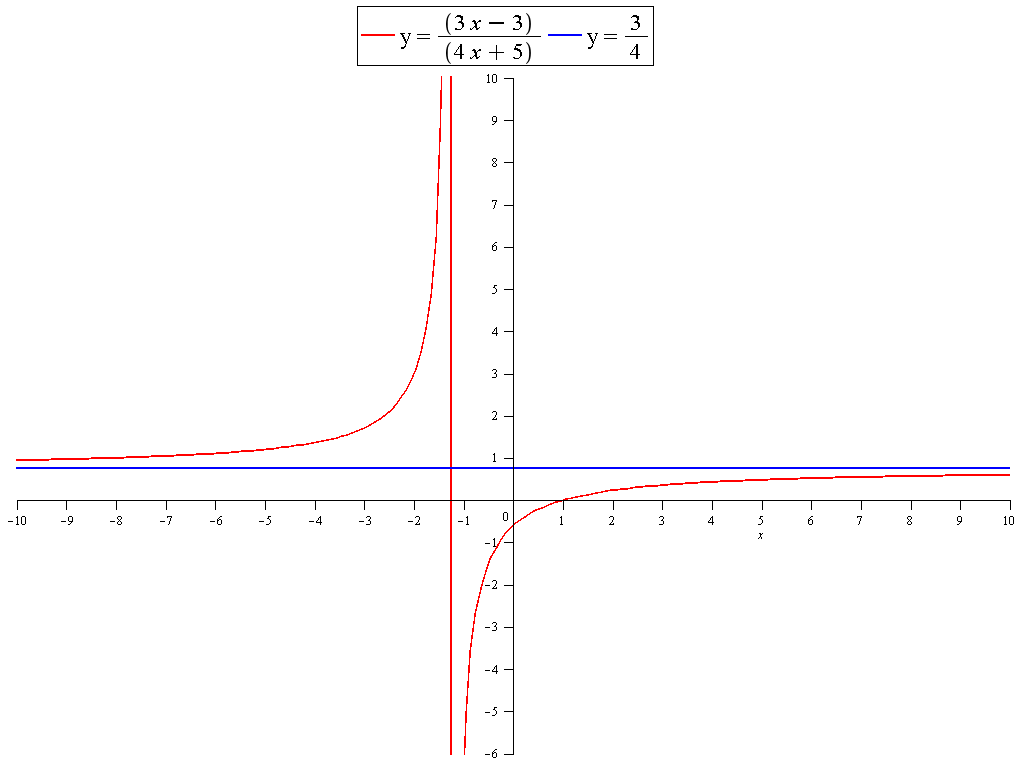
How do I determine the end behavior of the graph, f(x)=(3x-3)/(4x+5), in limit notation?
1 Answer
Apr 18, 2018
See below.
Explanation:
The end behaviour is what is happening as
Divide by
As before:
This shows that the line
So as
The graph of