Question

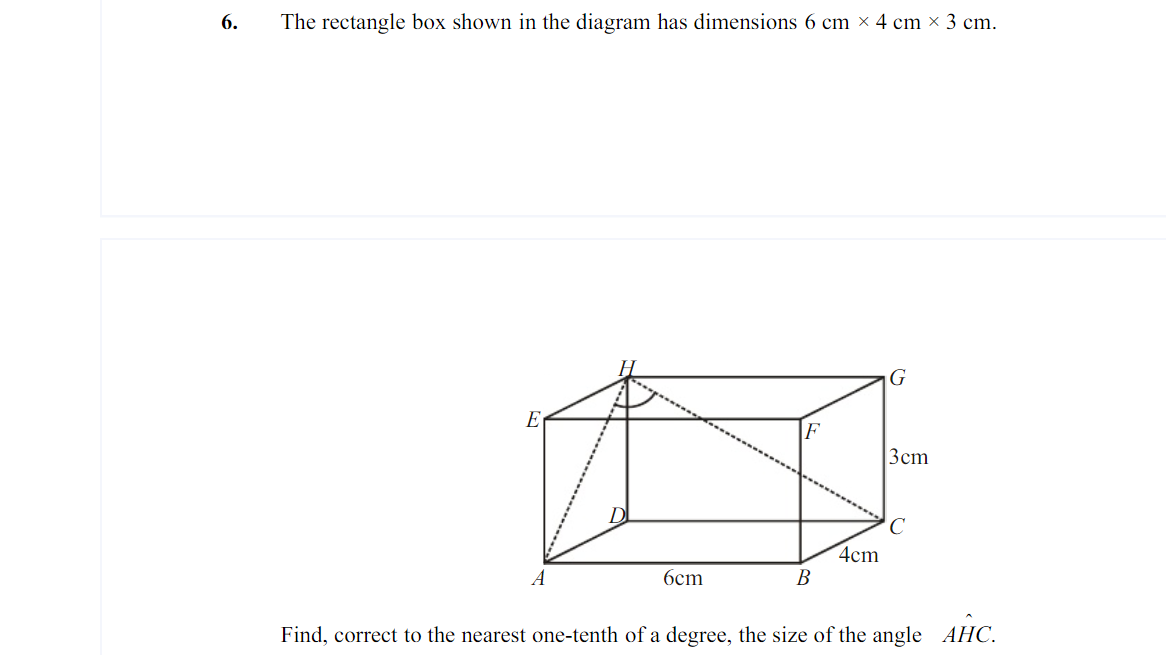
How do I find the angle of AHC?

Answer 1

`angle H=74.4` degrees

Explanation:

Not sure if I'm approaching this correctly, but it looks to me like you could make this into some right triangles: `DeltaHDA`, `DeltaHGC`, and `DeltaABC`.
In triangle `DeltaHDA`, you are looking for `HA` given `HD=3`, `DA=4`, and `angleD` is right, so using the Pythagorean Theorem: `(HD)^2+(DA)^2=(HA)^2`
`(HA)^2=25`
`(HA)=5`
Using the same process for the other triangles I mentioned (if you need me to expand it feel free to ask), `HC=6.708...` and `AC=7.211...`.

Therefore, you can use the Law of Cosines to find `angleH`:
`theta=cos^-1((a^2+b^2﹣c^2)/(2ab))` Substituting Values:
`angle H =cos^-1(((HA)^2+(HC)^2﹣(AC)^2)/(2(HA)(HC)))` Which simplifies to
`angle H=~74.44` (in degrees), rounded to the nearest tenth is
`angle H=74.4`